Question

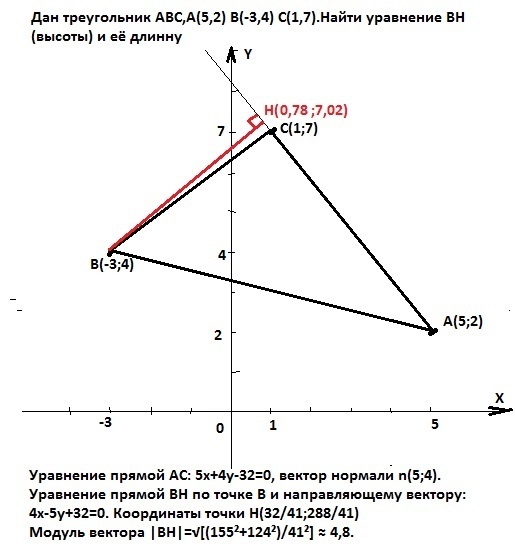
Дан треугольник ABC,A(5,2) B(-3,4) C(1,7).Найти уравнение BH(высоты) и её длинну

Answer 1

Дан треугольник ABC, A(5;2), B(-3;4), C(1;7). Найти уравнение BH(высоты) и её длину.Решение.Уравнение прямой АС по двум точкам:(X-Xa)/(Xc-Xa)=(Y-Ya)/Yc-Ya) или (X-5)/(-4)=(Y-2)/5 =>5X+4Y-32=0 (1) - уравнение прямой АС в общем виде с коэффициентами А=5, В=4, С=0 и D=-32.Вектор нормали (перпендикуляра) к этой прямой n(A;B) или n(5;4).Этот же вектор является направляющим вектором прямой ВН.Уравнение прямой ВН по точке В(-3;4) и направляющему вектору р(5;4):py(X-Xb)=px(Y-Yb) или 4(Х-(-3)=5(Y-4) =>4x-5y+32=0 (2) - это искомое уравнение прямой ВН.Длина вектора модуль) ВН=√[(Xh-Xb)²+(Yh-Yb)²].Координаты точки Н Xh и Yh находим, решая систему двух уравнений (1) и (2).5x+4y=32 |*4        25x+20y=1604x-5y+32  |*5 =>  16x-20y=128, отсюдах=32/41, y=(32-5х)/4=288/41.Тогда |BH|=√[(155²+124²)/41²]≈156,8/41≈4,8.
P.S. Задача чисто арифметическая, поэтому надо еще раз проверить арифметические действия. По построению, приложенному на рисунке, результат, похоже, верный.