Предмет: Математика,
автор: кристюша77
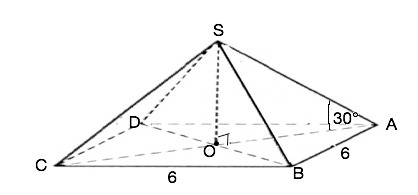
Длина стороны основания правильной четырехугольной пирамиды 6 см, а боковое ребро составляет с плоскостью основания угол 30°. Найдите объем пирамиды.
Ответы
Автор ответа:
0
Формула объёма пирамиды V=S•h:3, т.е. объём пирамиды равен одной трети произведения площади основания пирамиды на её высоту. Вершина правильной четырёхугольной пирамиды проецируется в центр её основания ( в точку пересечения диагоналей квадрата). Пусть пирамида SABCD. Диагонали квадрата равны и перпендикулярны друг другу и при пересечении делятся пополам. Т.к. сторона основания равна 6 см, то половина диагонали основания (из прямоугольного ∆(АОВ)) АО=АВ•sin45°=6•(√2/2)=3√2. По условию боковые ребра составляют с основанием 30°.
Рассмотрим прямоугольный ∆(ASО) Высота пирамиды - его катет SO=АО•tg30°=3√2•1/√3 . Домножив числитель и знаменатель на √3, получим SO=√6 => V=AB²•SO/3=36•√6/3=12√6 см³
Приложения:
Похожие вопросы
Предмет: Физика,
автор: bogdankatkov202040
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: tiktokzametki
Предмет: Литература,
автор: Халид8
Предмет: Биология,
автор: Аноним