Предмет: Математика,
автор: никита3400
Математики помогите плииз!!
Приложения:

Ответы
Автор ответа:
0
1) а) 

б)![y=3 sqrt[3]{x}+ sqrt{x}*arcsin^3(x) + 3LN(4-x^2) y=3 sqrt[3]{x}+ sqrt{x}*arcsin^3(x) + 3LN(4-x^2)](https://tex.z-dn.net/?f=y%3D3+sqrt%5B3%5D%7Bx%7D%2B+sqrt%7Bx%7D%2Aarcsin%5E3%28x%29+%2B+3LN%284-x%5E2%29)

в)
В таком виде производную брать удобнее.

2)


3)
Экстремум

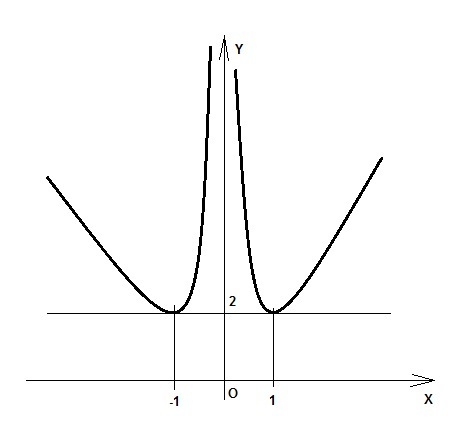
x1 = -1; y(-1) = 1 + 1/1 = 2
x2 = 1; y(1) = 1 + 1/1 = 2
Кроме того, есть точка разрыва x = 0. Неустранимый разрыв 2 рода.
При x < -1 будет y' < 0, функция убывает.
При x ∈ (-1; 0) будет y' > 0, функция возрастает.
x = -1 - точка минимума
При x ∈ (0; 1) будет y' < 0, функция убывает.
При x > 1 будет y' > 0, функция возрастает.
x = 1 - точка минимума
График прилагается.
б)
в)
В таком виде производную брать удобнее.
2)
3)
Экстремум
x1 = -1; y(-1) = 1 + 1/1 = 2
x2 = 1; y(1) = 1 + 1/1 = 2
Кроме того, есть точка разрыва x = 0. Неустранимый разрыв 2 рода.
При x < -1 будет y' < 0, функция убывает.
При x ∈ (-1; 0) будет y' > 0, функция возрастает.
x = -1 - точка минимума
При x ∈ (0; 1) будет y' < 0, функция убывает.
При x > 1 будет y' > 0, функция возрастает.
x = 1 - точка минимума
График прилагается.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: sofiasizonenko139
Предмет: Математика,
автор: aminrazakov63
Предмет: Алгебра,
автор: irinacekalina8233
Предмет: Геометрия,
автор: Aleksanyan1111