Предмет: Математика,
автор: sphynx7
Вычислите неопределенный интеграл методом замены переменной.
Нужно подробное решение.
Приложения:
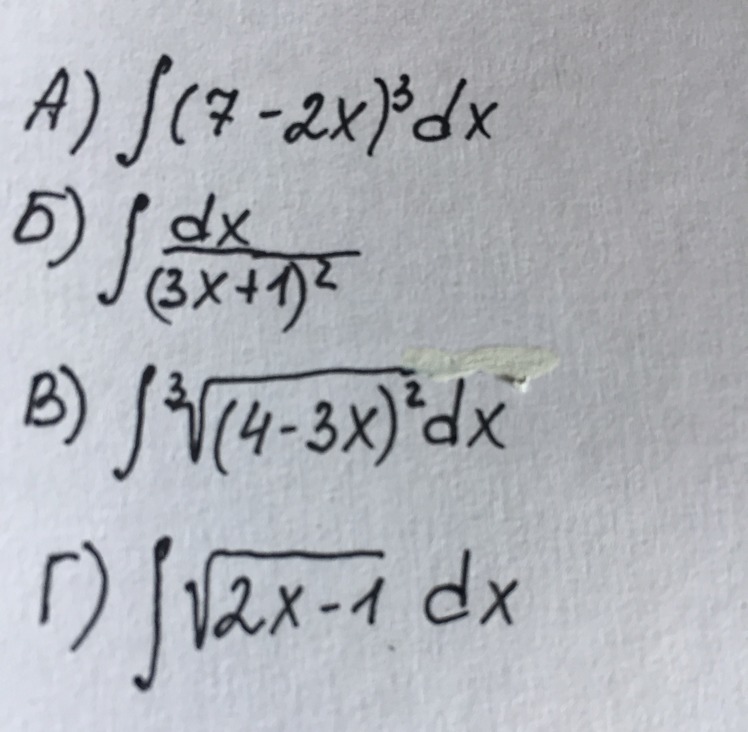
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: katyashigina90
Предмет: Математика,
автор: davlashield
Предмет: Алгебра,
автор: mneizmajlov
Предмет: Химия,
автор: manulkina2000
Предмет: Математика,
автор: petrushina1986