Предмет: Математика,
автор: Лен44
Помогите пожалуйста найти sin x если cos x=
Приложения:
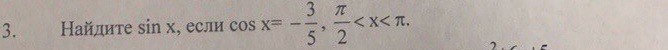
Ответы
Автор ответа:
1
Основное тригонометрическое тождество:

Отсюда следует, что



Так как синус положителен на промежутке от пи пополам до пи, то

Отсюда следует, что
Так как синус положителен на промежутке от пи пополам до пи, то
Лен44:
в ответе писать sin x=4\5 ?
Да
Похожие вопросы
Предмет: Литература,
автор: karolino4ka10
Предмет: История,
автор: salomovildar
Предмет: Математика,
автор: vladislavakvitcuk
Предмет: Английский язык,
автор: blockstrike22802
Предмет: Русский язык,
автор: Аноним