Предмет: Математика,
автор: unknownunknown2
Решите хоть что-нибудь пожалуйста
Приложения:
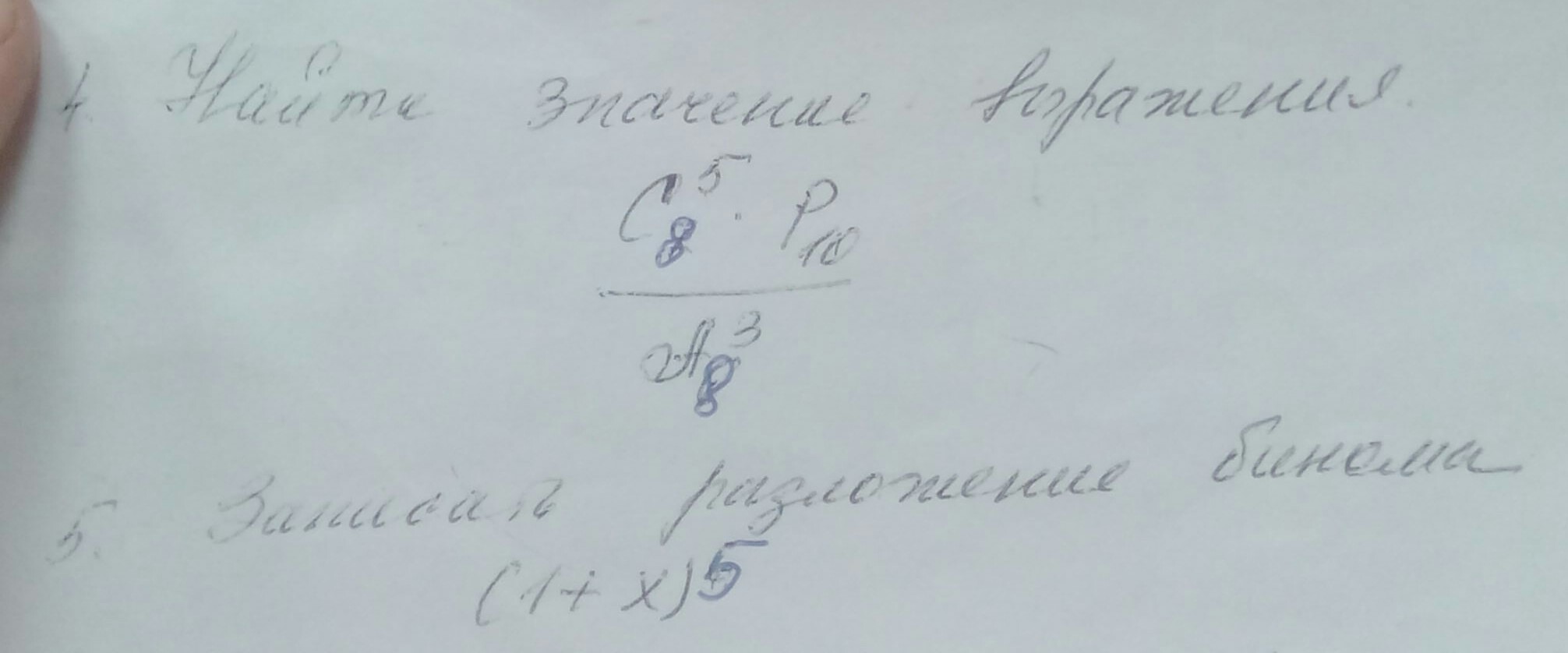
Ответы
Автор ответа:
0
Формула разложения бинома Ньютона
при a=1, b=x, n=5
Похожие вопросы
Предмет: Химия,
автор: nellieeeeee
Предмет: Українська мова,
автор: vikylka353
Предмет: Другие предметы,
автор: olegjovter
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: Аноним