Question

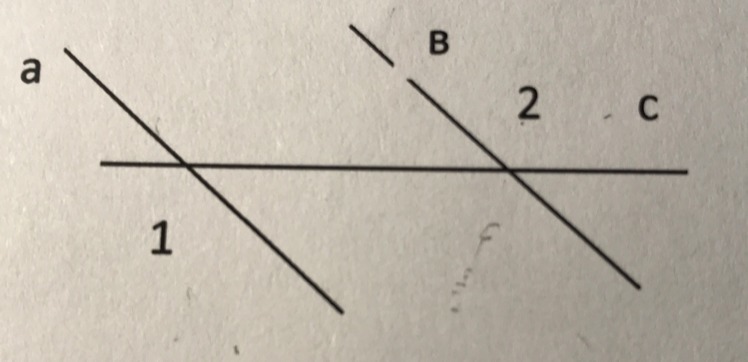
1. Прямые а и в параллельны. Угол 1 равен 145°. Найдите сумму ушла 1 и 2 (в градусах).
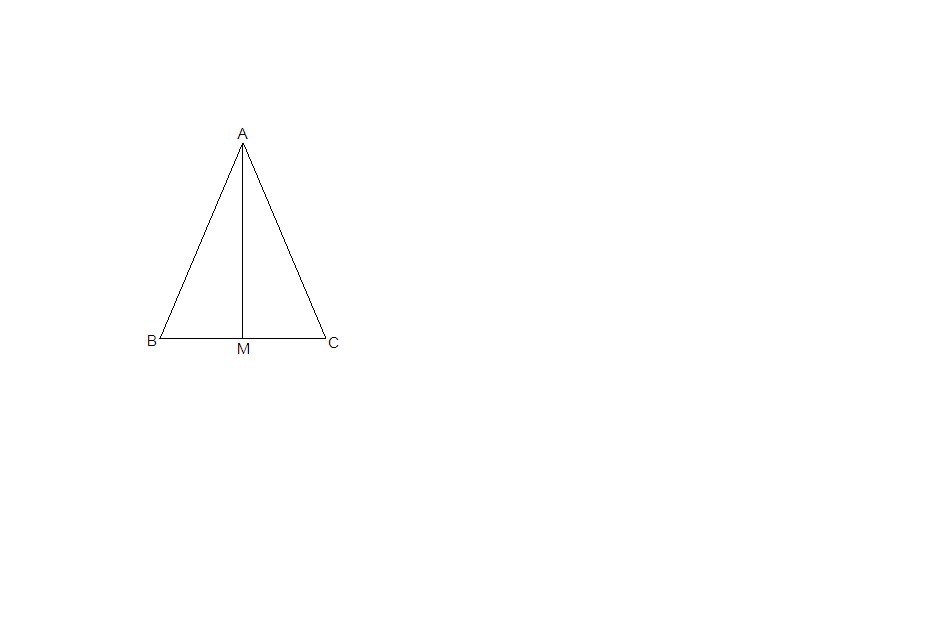
2. Биссектриса угла А равнобедренного треугольника ABC пересекает основание в точке М. Найдите длину отрезка АМ, если периметры треугольников ABC и ABM равны 32 и 24 соотвественно.

Answer 1

1.
∠1 = ∠2 = 145°
∠1 + ∠2 = 290°

2.
АМ - биссектриса равнобедренного треугольника, проведенная к основанию, значит АМ и высота и медиана.
ΔABM = ΔACM по катету и гипотенузе (АМ - общий катет, АВ = АС, т.к. треугольник равнобедренный)
Pabm = Pamc = 24см
Pabm = AB + BM + AM
2Pabm = 2(AB + BM + AM) = 2AB + 2BM + 2 AM
Т.к. 2ВМ = ВС, а 2АВ = АВ + АС, получаем:
2Pabm = AB + AC + BC + 2AM = Pabc + 2AM
48 = 32 + 2AM
2AM = 16
AM = 8