Предмет: Алгебра,
автор: Krates752
Решить уравнение:
cosX+cos7X=√3 cos4X
Приложения:

Ответы
Автор ответа:
0
Автор ответа:
0
Решение в приложении.
Приложения:
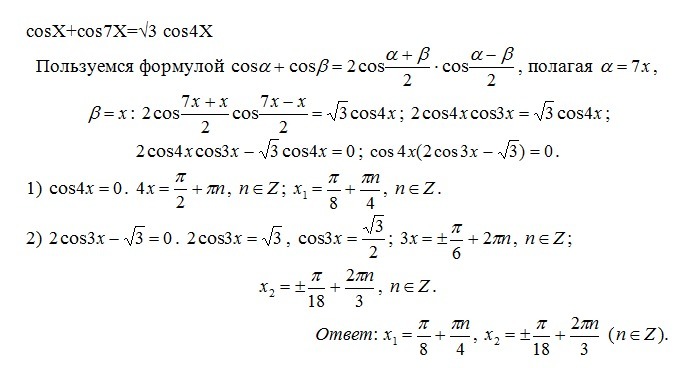
Похожие вопросы
Предмет: Литература,
автор: aniafominykh
Предмет: Литература,
автор: brosasha20
Предмет: Английский язык,
автор: koganelizaveta5
Предмет: Математика,
автор: Анна223367