Question

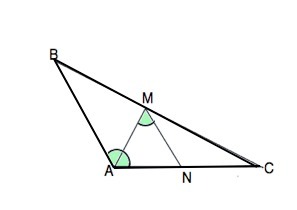
отрезок АМ -биссектриса треугольника АВС.Через точку М проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке N.Найти углы треугольника AMN,если угол ВAC=122

Answer 1

AB║MN, значит ∠BAM=∠KMN как внутрение разностронии, ∠BMA=∠MAN тоже, но так как AM - биссектриса, тогда они между собой тоже ровны. Это значит что ∠AMN: равнобедренный так как углы при боковых сторонах равны, по 61°. А потом ∠ANM=58°

Answer 2

Биссектриса АМ делит уол ВАС пополам. ⇒  

ВАМ=МАN=122°2=61°. 

MN║АВ, АМ секущая при параллельных прямых, следовательно,  ∠ВАМ=∠АМN как накрестлежащие. 

Так как ∠МАВ∠MAN, то

 ∠МАN=∠AMN=61°

 Из суммы углов треугольника находим

 ∠ANM= 180°-2•61°=58°