Question

Решите, пожалуйста, эту задачу. Заранее БОЛЬШОЕ спасибо!

Answer 1

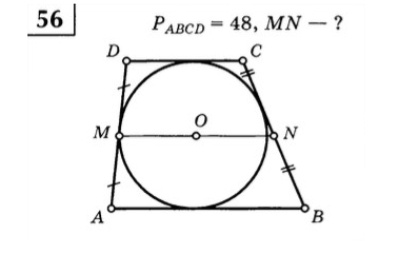
для четырехугольника, в который вписана окружность справедливо следующее - суммы длин противоположных сторон попарно равны
АВ+СД=АД+СВ
Р=АВ+СД+АД+СВ=(АВ+СД)*2
(АВ+СД)=P/2
MN=(АВ+СД)/2=P/4=48/4=12 - это ответ

Answer 2

Вписать окружность в четырехугольник можно только в том случае, если суммы противоположных сторон равны. DC + AB = DA + CB
пусть CN и BN = х, а DM + AM =y
тогда CB+DA = x+x+y+y=2x+2y=2(x+y)
тогда DC+AB тоже 2(х+у)
тогда общее уравнение: 2х+2у±2х+2у=48
4х+4у=48
4(х+у)=48
2*(х+у)=24
сумма противоположных сторон равна 24
MN - средняя линия, она равна половине суммы оснований, т.е. 24:2=12