Предмет: Математика,
автор: Щах
Решить интеграл методом тригонометрических функций
Приложения:
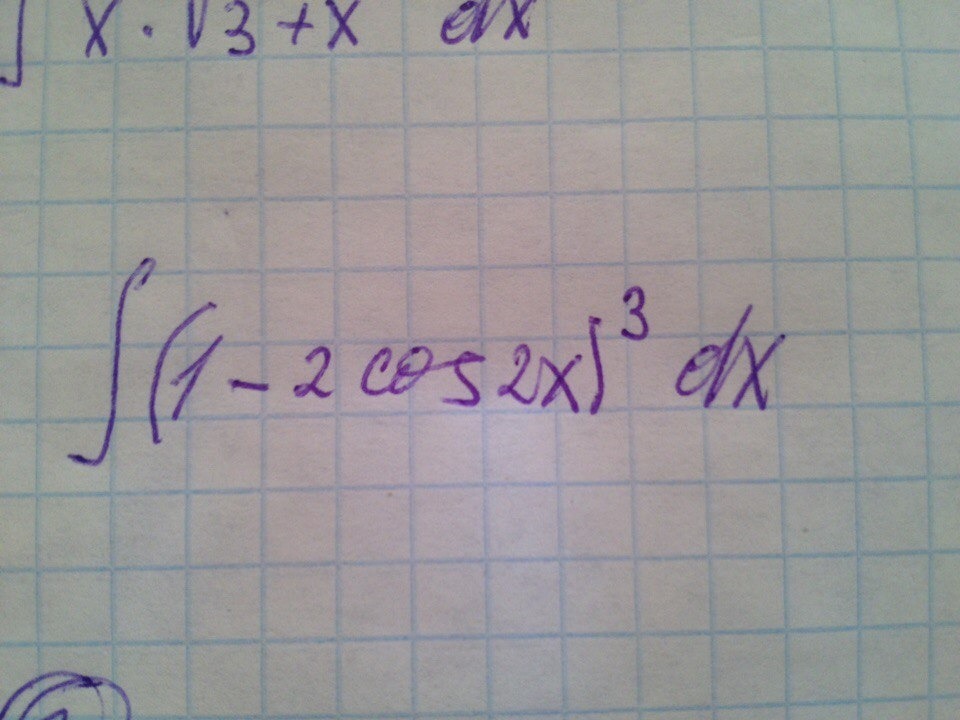
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: anelia1official
Предмет: Алгебра,
автор: anelia1official
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: GONACe
Предмет: Математика,
автор: Irkakostenko198