Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, решить уравнения.
Приложения:
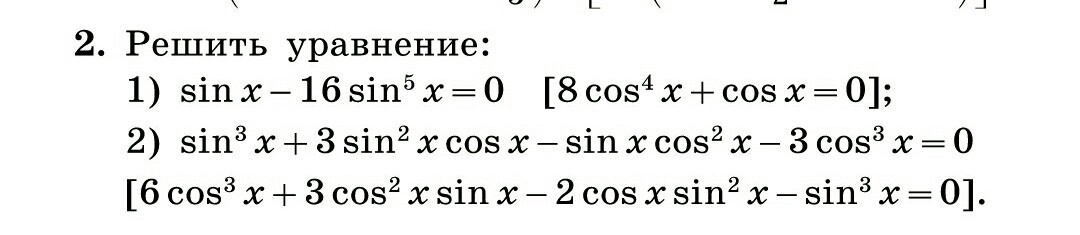
Ответы
Автор ответа:
0
Второе задание
Автор ответа:
0
спасибо большое
Похожие вопросы
Предмет: Другие предметы,
автор: htykjfy
Предмет: Геометрия,
автор: oia92149
Предмет: Другие предметы,
автор: ilonamarchenko210620
Предмет: Алгебра,
автор: dekeva
Предмет: История,
автор: Bocsineanu