Предмет: Алгебра,
автор: sovu
СРОЧНО помогите с логарифмом
Приложения:
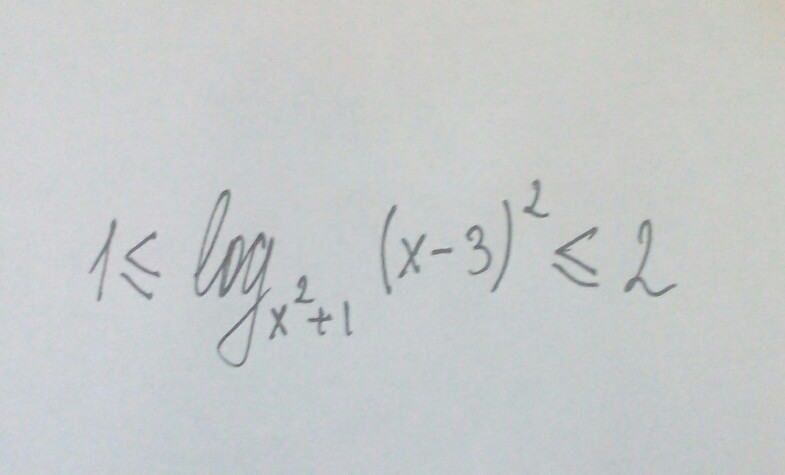
Ответы
Автор ответа:
0
1≤ ㏒ₓ²₊₁(х-3)² ≤2 ОДЗ х≠0 , х-3≠0 ⇒ х≠3
так как х²+1>1 при любом х не равном 0 , знак неравенства при решении не меняется
㏒ₓ²₊₁(х-3)²≥1
(х-3)² ≥ х²+1
х²-6х+9≥ х²+1
-6х +8 ≥0
х≤ 4/3
㏒ₓ²₊₁(х-3)² ≤2
(х-3)² ≤ (х²+1)²
1) х-3 ≤ х²+1 данное неравенство выполняется при любом значении х
2) х-3 ≥ -х²-1
х²+х-2≥0
D=1+8=9
x₁=(-1+3)/2=1
x₂=(-1-3)/2=-2
определим знаки
+ - +
_________-2________1______________
х∈(-∞;-2]∪[1;+∞)
ответ с учетом ОДЗ х∈(-∞;-2)∪(1;4/3]
так как х²+1>1 при любом х не равном 0 , знак неравенства при решении не меняется
㏒ₓ²₊₁(х-3)²≥1
(х-3)² ≥ х²+1
х²-6х+9≥ х²+1
-6х +8 ≥0
х≤ 4/3
㏒ₓ²₊₁(х-3)² ≤2
(х-3)² ≤ (х²+1)²
1) х-3 ≤ х²+1 данное неравенство выполняется при любом значении х
2) х-3 ≥ -х²-1
х²+х-2≥0
D=1+8=9
x₁=(-1+3)/2=1
x₂=(-1-3)/2=-2
определим знаки
+ - +
_________-2________1______________
х∈(-∞;-2]∪[1;+∞)
ответ с учетом ОДЗ х∈(-∞;-2)∪(1;4/3]
Автор ответа:
0
(х-3)² ≤ (х²+1)² в этом месте
Автор ответа:
0
и не рассмотрели этот случай x-3>=-x^2-1
Автор ответа:
0
одз меняется на (-беск., -2]U[1;4/3)
Автор ответа:
0
спасибо за замечание ))
Автор ответа:
0
:)
Похожие вопросы
Предмет: Обществознание,
автор: violettatashlanova
Предмет: Русский язык,
автор: nikit9772
Предмет: Химия,
автор: sidenkovika2007
Предмет: Алгебра,
автор: Рожденныйползать