Question

Высота параллелограмма имеет длину,равную 5 корень из 6. Равнобедренный треугольник, боковая сторона которого равна 7, а высота, проведённая к основанию, равна 5, имеет такую же площадь, что и параллелограмм.Найдите длину стороны параллелограмма,к которой проведена высота.

Answer 1

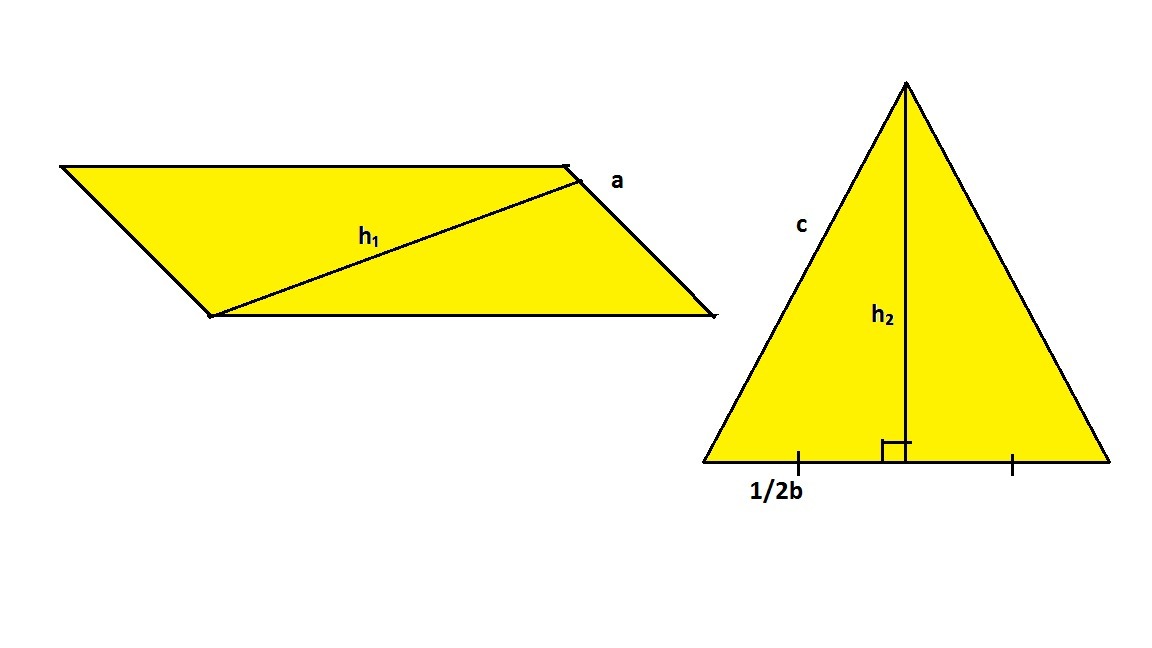
Пусть h₁ - высота параллелограмма, a - его основание, b - основание равнобедренного треугольника, h₂ - высота равнобедренного треугольника, c - его боковая сторона.
Площадь параллелограмма равна произведению основания на высоту:
$S = h_{1}a = 5 sqrt{6} a$
В равнобедренном треугольника высота, проведённая к основанию, является медианой и биссектрисой.
По теореме Пифагора (рассматривается треугольник, образованный высотой, а не весь равнобедренный треугольник):
$dfrac{1}{2}b = sqrt{c^2 - h_{2}^{2}} = sqrt{7^2 - 5^2} = sqrt{49 - 25} = sqrt{24} = 2 sqrt{6}$
Тогда $b = 4 sqrt{6}$
Площадь треугольника равна половине произведения основания на высоту:
$S = dfrac{1}{2}bh_{2} = dfrac{1}{2} cdot 4 sqrt{6 } cdot 5 = 10 sqrt{6}$
Т.к. площади треугольника и параллелограмма равны, то
$5 sqrt{6} a = 10 sqrt{6} = textgreater a = dfrac{10 sqrt{6} }{5 sqrt{6} } = 2$
Ответ: 2.