Предмет: Алгебра,
автор: Alen198
Вычислить предел функций, используя правило Лопиталя
(Пример 6.5 а и б)
Приложения:

Ответы
Автор ответа:
0
Приложения:
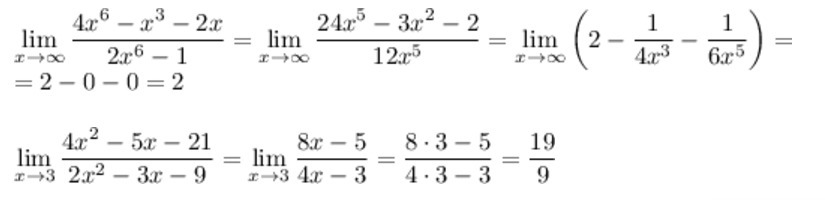
Автор ответа:
0
а)
lim (4x^6 - x^3 - 2x)/(2x^6 - 1) = lim (24x^5 - 3x^2 - 2)/12x^5 = lim (120x^4 - 6x)/60x^4 = lim (480x^3 - 6)/240x^3 = lim 1440x^2 / 720x^2 = 1400/720 = 2
б)
lim (4x^2 - 5x - 21)/(2x^2 - 3x - 9) = lim (8x - 5) / (4x - 3) = {x -> 3} = (24 - 5) / (12 - 3) = 19/9
{вообще, первый предел просто равен отношению старших степеней = 4/2, а во втором (4x^2 - 5x - 21)/(2x^2 - 3x - 9) = (4x + 7)(x - 3) / (2x + 3)(x - 3) = (4x + 7)/(2x + 3) = 19/9}
lim (4x^6 - x^3 - 2x)/(2x^6 - 1) = lim (24x^5 - 3x^2 - 2)/12x^5 = lim (120x^4 - 6x)/60x^4 = lim (480x^3 - 6)/240x^3 = lim 1440x^2 / 720x^2 = 1400/720 = 2
б)
lim (4x^2 - 5x - 21)/(2x^2 - 3x - 9) = lim (8x - 5) / (4x - 3) = {x -> 3} = (24 - 5) / (12 - 3) = 19/9
{вообще, первый предел просто равен отношению старших степеней = 4/2, а во втором (4x^2 - 5x - 21)/(2x^2 - 3x - 9) = (4x + 7)(x - 3) / (2x + 3)(x - 3) = (4x + 7)/(2x + 3) = 19/9}
Приложения:
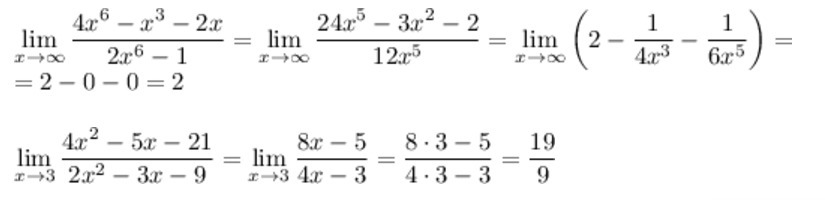
Похожие вопросы
Предмет: Химия,
автор: alyana5
Предмет: Математика,
автор: zambulbekovabanu
Предмет: Литература,
автор: bv159493
Предмет: Математика,
автор: alisararan03
Предмет: Алгебра,
автор: dudukin