Question

В угол,величина которого составляет 60 градусов,вписаны два круга,которые внешне соприкасаются друг к другу. Найдите радиус большего из них,если радиус меньшего равна 6 см.

Answer 1

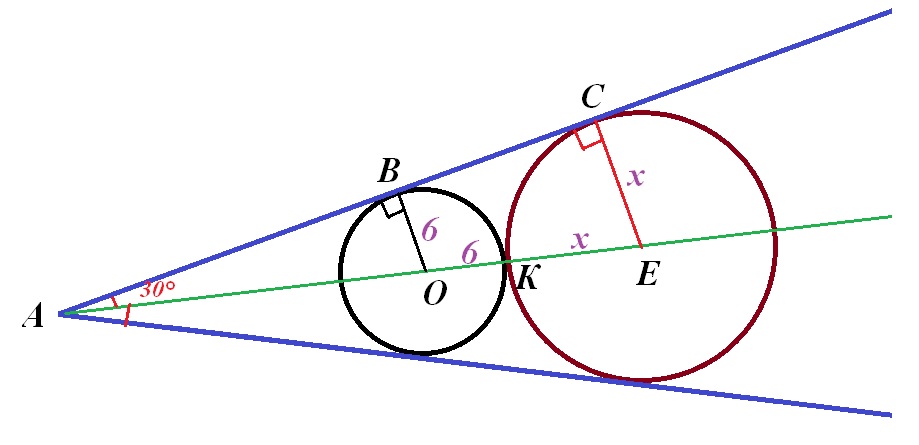
Чертеж во вложении.
Пусть точки В и С - это точки касания окружностей одной из сторон угла А.
Т.к. две окружности касаются друг друга внешним образом (К - точка касания) и вписаны в угол А, то центры окружностей - точки О и Е - лежат на биссектрисе угла А.
Значит, ∠САЕ=30°.
По свойству касательной радиус ОВ⊥АС и радиус ЕС⊥АС.
Пусть ЕС=х см, тогда ЕК=х см и ОЕ=6+х см.
В прямоугольном ∆АОВ АО = 2ОВ=2*6=12 см (гипотенуза и катет в треугольнике с углом в 30°)
Прямоугольные ∆АОВ и ∆АЕC подобны по двум углам.
Значит, 
$dfrac{AO}{OB}=dfrac{AE}{EC} => dfrac{12}{6}=dfrac{12+6+x}{x} => x=18\\ CE=18$
Ответ: 18 см.