Предмет: Геометрия,
автор: Shark171299
биссектрисы углов a и b равностороннего треугольника abc пересекаются в точке o. найдите длину перпендикуляра, опущенного из точки o на сторону треугольника, если ao = 6 см
Ответы
Автор ответа:
0
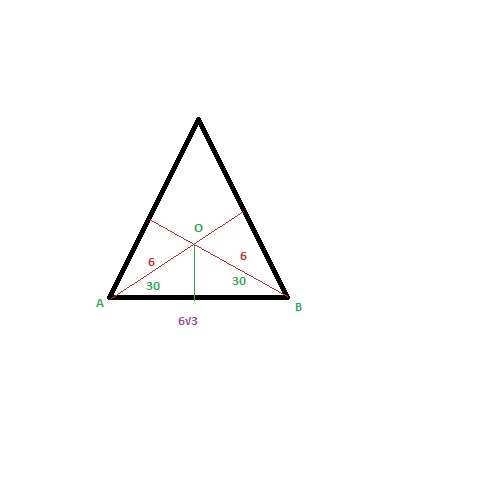
Если треуг. равносторонний, то его углы =60 град.Проведём из точки О перпендикуляры к сторонам. Они все равны, т.к. являются радиусами вписанной окрружности. Перпендикуляр из т. О к АС обозначим ОН.Рассм. треуг-к АОН: уголОНА=90.
УголОАН=30 град., АО=6.
Радиус (он же катет) ОН=АО*sin30=6*1/2=3
УголОАН=30 град., АО=6.
Радиус (он же катет) ОН=АО*sin30=6*1/2=3
Автор ответа:
0
треугольник АОВ получается равнобедреным, а углы при основании равны 30 градусам, угол АОВ равен 180-60=120 градусам
основание равно 2а*cosa=2*6*cos30=6*√3
Так как перпендикуляридёт под прямым углом образуется прямоугольный треугольник, где гипотенуза равна 6, а углы 30, 60 и 90 градусов.
Сторона напротив угла 30 градусов в прямоугольном треугольнике равна половине гипотенузы
6:2=3
Ответ: перпендикуляр равен 3
основание равно 2а*cosa=2*6*cos30=6*√3
Так как перпендикуляридёт под прямым углом образуется прямоугольный треугольник, где гипотенуза равна 6, а углы 30, 60 и 90 градусов.
Сторона напротив угла 30 градусов в прямоугольном треугольнике равна половине гипотенузы
6:2=3
Ответ: перпендикуляр равен 3
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: sasha92929296
Предмет: Русский язык,
автор: OlegSac
Предмет: Геометрия,
автор: semaru220
Предмет: Геометрия,
автор: Сердж
Предмет: Алгебра,
автор: RapunZzzel