Предмет: Алгебра,
автор: Аноним
Нужно доказать,что данное число-натуральное)
1.) и 2)
(тут 2 идентичных задания).Объясните пожалуйста только,как вы решаете)заранее спасибо)
Приложения:
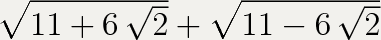
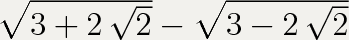
Ответы
Автор ответа:
0
Применяем формулу  .
.
Только вот a и b отыскиваем подбором. Хотя можно их найти, решив систему уравнений, но мне легче подбором.


Как видим, все значения - натуральные числа.
Только вот a и b отыскиваем подбором. Хотя можно их найти, решив систему уравнений, но мне легче подбором.
Как видим, все значения - натуральные числа.
Похожие вопросы
Предмет: Алгебра,
автор: ghopka
Предмет: Алгебра,
автор: FlipaVika2
Предмет: Биология,
автор: roho3963
Предмет: Литература,
автор: Лентяка