Предмет: Алгебра,
автор: ArturcheG
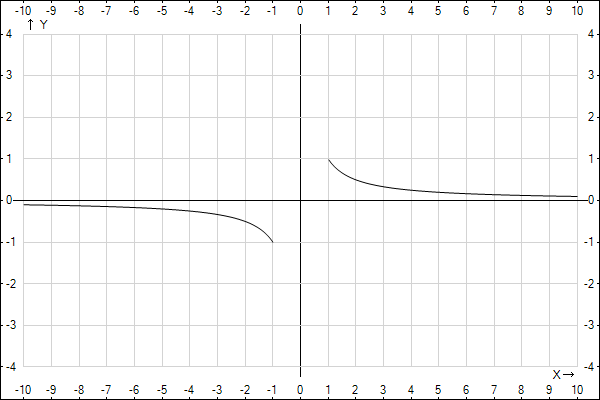
построить график функции y= Sin(arcSin 1/x)
Ответы
Автор ответа:
0
1.
2.
3.
четная
4.
(-1;-1), (1;1) - точки разрыва.
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: bespalyynataha
Предмет: Физика,
автор: FedorRyzkhov
Предмет: Алгебра,
автор: niklaskov
Предмет: Химия,
автор: Arllikin
Предмет: Математика,
автор: radikdemon