Question

На стороне AB треугольника ABC с углами A=30 и B=130 как на диаметре построен круг. Найдите площадь части этого круга, лежащей внутри треугольника

Answer 1

Согласно теории площадь круга зависит от радиуса этого круга и связана с радиусом формулой S=π·r². Следовательно, часть круга также хависит от радиуса этого круга.

По сему, непонятно, по какой причине автор не указал явно или неявно на радиус.

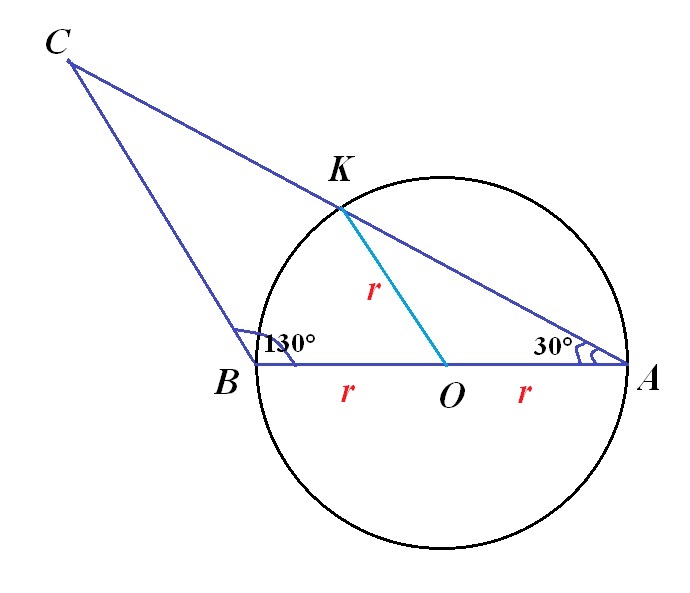
Пусть r-радиус круга, тогда в ∆АВС сторона АВ=2r.

Проведем еще один радиус ОК. Тогда требуемая площадь может быть найдена как сумма площади ∆АОК и площади сектора КОВ.

∆ОАК - равнобедренный с основанием АК, тогда ∠АОК=180°-(30°+30°)=120°.

S ∆АОК = ½ OA·OK·sin∠АОК= ½ r²·sin120°= ½ r²·sin60°= (r²·√3)/4.

∠ВОК и ∠АОК - смежные.

∠ВОК=180°-120°=60°

Площадь сектора КОВ:

$S_{cek}=frac{pi r^2alpha}{360}=frac{pi r^2*60}{360}=frac{pi r^2}{6}$

Итак, площадь части круга, лежащей внутри треугольника, есть

$frac{r^2sqrt3}{4}+frac{pi r^2}{6}=frac{r^2}{12}(3sqrt3+2pi)$

Автору останется выяснить, чему равен радиус r круга, и поставить в последнее выражение.