Предмет: Алгебра,
автор: viiiii
Решите кто нибудь. Пожалуйста.
Приложения:
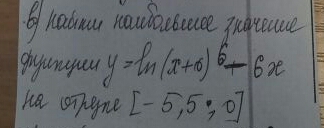
Ответы
Автор ответа:
0
y=ln(x+6)^6-6x = 6ln(x+6)-6x на отрезке[-5,5;0]
Производная
y'= 6/(x+6) -6
Находим экстремумы
y'= 0 6/(x+6) -6 = 0
1/(x+6) = 1
x+6 = 1
x = -5
Знаки производной на числовой оси
+ 0 -
--------------!--------------
-5
Следовательно в точке х =- 5 функция имеет локальный максимум y(-5) = 6ln(-5+6) -6*(-5) = 6 ln(1) +30 =30
Значение функции на границах отрезка
y(-5,5) =6ln(0,5) -6*(-5,5) = 33-6ln(0,5) =28,8
y(0) =6ln(6) -6*(6) = 6ln(6) =10,8
Окончательно максимальное значения функция принимает в точке х = -5 у(-5) = 30
Похожие вопросы
Предмет: Английский язык,
автор: sisupertop
Предмет: Обществознание,
автор: Smeepy
Предмет: Информатика,
автор: KatyDM
Предмет: Литература,
автор: spra