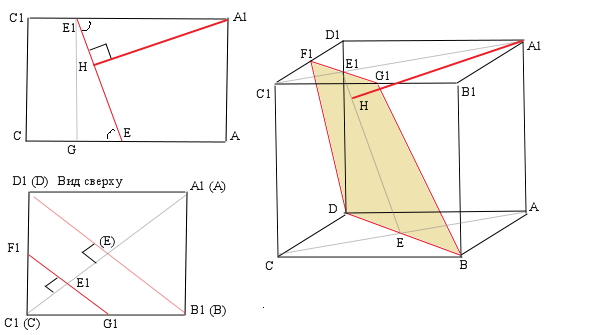
Ребро куба ABCDA1B1C1D1 равно 2. Найдите расстояние от точки A1 до плоскости, проходящей через точку B, и середины ребер D1C1 и B1C1.
C чертежом пожалуйста.
Ответы
плоскость-сечение ---равнобокая трапеция BDF1G1
расстояние от точки до плоскости ---перпендикуляр => нужно построить плоскость, перпендикулярную трапеции...
это будет диагональное сечение куба A1ACC1 ---прямоугольник...
искомое расстояние А1Н
обозначим ребро куба (а)
треугольники A1E1H и EE1G подобны (они прямоугольные по построению,
углы A1E1H и GEE1 равны как накрестлежащие при параллельных прямых АС и А1С1 и секущей ЕЕ1) => А1Н / Е1G = А1Е1 / ЕЕ1
А1Н = Е1G * А1Е1 / ЕЕ1
Е1G = СС1 = а
А1Е1 = (3/4) * А1С1 (диагонали основания-квадрата перпендикулярны и точкой пересечения делятся пополам, треугольники D1B1C1 и F1G1C1 подобны с коэффициентом подобия 2 / 1 => С1Е1 = С1А1 / 4 )
по т.Пифагора А1С1 = а*V2
А1Е1 = 3а*V2 / 4
ЕЕ1 ---высота трапеции с бОльшим основанием = а*V2,
меньшим основанием = а*V2 / 2 (средняя линия треугольника D1B1C1),
боковой стороной = корень(a^2 + (a/2)^2) = a*V5 / 2 (по т.Пифагора)
по т.Пифагора ЕЕ1^2 = (a*V5 / 2)^2 - ((а*V2 - а*V2 / 2)/2)^2 = 5a^2 / 4 - a^2 / 8 = 9a^2 / 8
ЕЕ1 = 3а / (2*V2) = 3a*V2 / 4
получилось, что ЕЕ1 = А1Е1 =>
А1Н = E1G = а
A1H = 2
как-то так...