Question

высота правильной шестиугольной призмы равна а. Диагонали двух смежных боковых граней ,проведённых из одной вершины,взаимно перпендикулярны .Определить боковую поверхность призмы

Answer 1

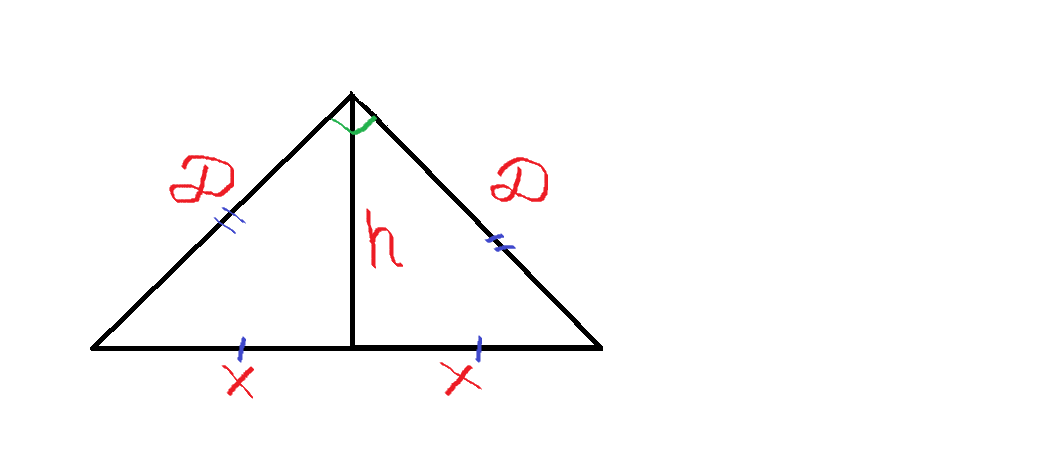
Так как две смежные диагонали перпендикулярны друг другу, получаем прямоугольный треугольник во вложении:

Тогда

 $h=sqrt{D^2+x^2}$

 $2x=sqrt{D^2+D^2}=Dsqrt2$

Откуда получаем $x=frac{Dsqrt2}{2}$

Тогда получаем

$h=sqrt{D^2+x^2}=sqrt{D^2+(frac{Dsqrt2}{2})^2}=sqrt{frac{3D^2}{2}}$

$D^2=frac23h^2$

 $D=frac{2x}{sqrt2}=xsqrt2$

 $2x^2=frac23h^2$

 $x=frac{h}{sqrt3}}$

Площадь боковой поверхности считаем по формуле: периметр основания на высоту:

 $S=P*h$

 Периметр равен:

$P=frac{6h}{sqrt3}=2hsqrt3$

Тогда площадь боковой поверхности будет равна:

 $S=Ph=2hsqrt3*h=2h^2sqrt3$