Question

Можно ли прямоугольник, составленный из равных квадратиков, разрезать на фигурки, состоящие из четырёх квадратиков и имеющие форму буквы Г, если пря- моугольник имеет размеры: 1) 1612 квадратиков; 2) 1516 квадратиков; 3) 8(mn) квадратиков, где m > 1, n > 1?

Answer 1

Для начала, посмотрим, какие маленькие прямоугольники можно составить из фигурок, составленных из квадратиков, имеющих форму буквы Г:
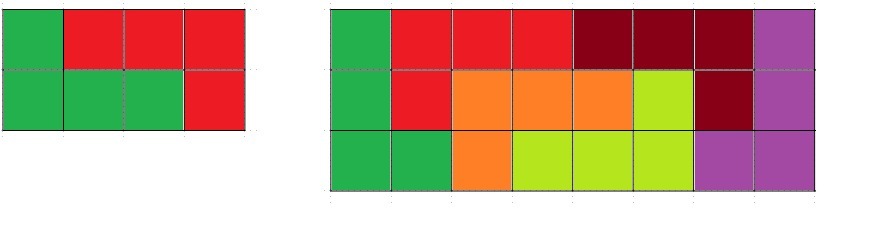
4x2 и 8x3 (на рисунке)
1)
Прямоугольниками 4x2 можно замостить прямоугольник 16x12
(Один из вариантов - размещать все прямоугольники 4x2 так, чтобы они были ориентированы одинаково. Параллельными сделать стороны 4 и 16 прямоугольников 4x2 и 16x12. Тогда будет 12 : 2 = 6 рядов по 16 : 4 = 4 прямоугольника)
А каждый из маленьких прямоугольников разбивать на два уголка из 4 клеток (из условия) мы умеем.

2)
Таким же образом, как и в пункте 1 можно найти разбиение прямоугольника 15x16 на прямоугольники 3x8. Будет 16 : 8 = 2 ряда по 15 : 3 = 5 прямоугольников.

3)
Если 8(m x n) означает, что это прямоугольник 8m x 8n, то можно разбить на прямоугольники 4x2 (2m рядов по 4n прямоугольников(

Если 8(mxn) означает, что это прямоугольник q x w, причем q*w делится на 8, то возможно несколько вариантов:
Либо q делится на 4, а w делится на 2 (аналогично w делится на 4, а q делится на 2), тогда можно разделить на q рядов по w прямоугольников 4x2 (аналогично w рядов по q прямоугольников 4x2)
Либо q делится на 8 (аналогично w делится на 8 рассмотрим только вариант q делится на 8 не нарушая общности). Так как w>1, то можно выделить прямоугольник q x 3, Который можно замостить прямоугольниками 8x3 (так как q делится на 8). Отрежем от нашего прямоугольника с краю прямоугольник q x 3. Останется прямоугольник q x 2p, где p≥0. Теперь (если p≠0) можно вернуться к варианту, где q делится на 4, а w делится на 2. Действительно, q делится на 8, а значит и на 4, а 2p делится на 2. А значит оставшийся прямоугольник также можно разбить на фигурки из условия

Ответ:
1) да
2) да
3) да