Предмет: Геометрия,
автор: carrot4
Боковые стороны равнобедренной трапеции при их продолжении пересекаются под прямым углом. Найти все стороны трапеции, если её площадь равна 12 см², а высота равна 2 см. Даю 50 баллов. За СПАМ бан!!!
Ответы
Автор ответа:
0
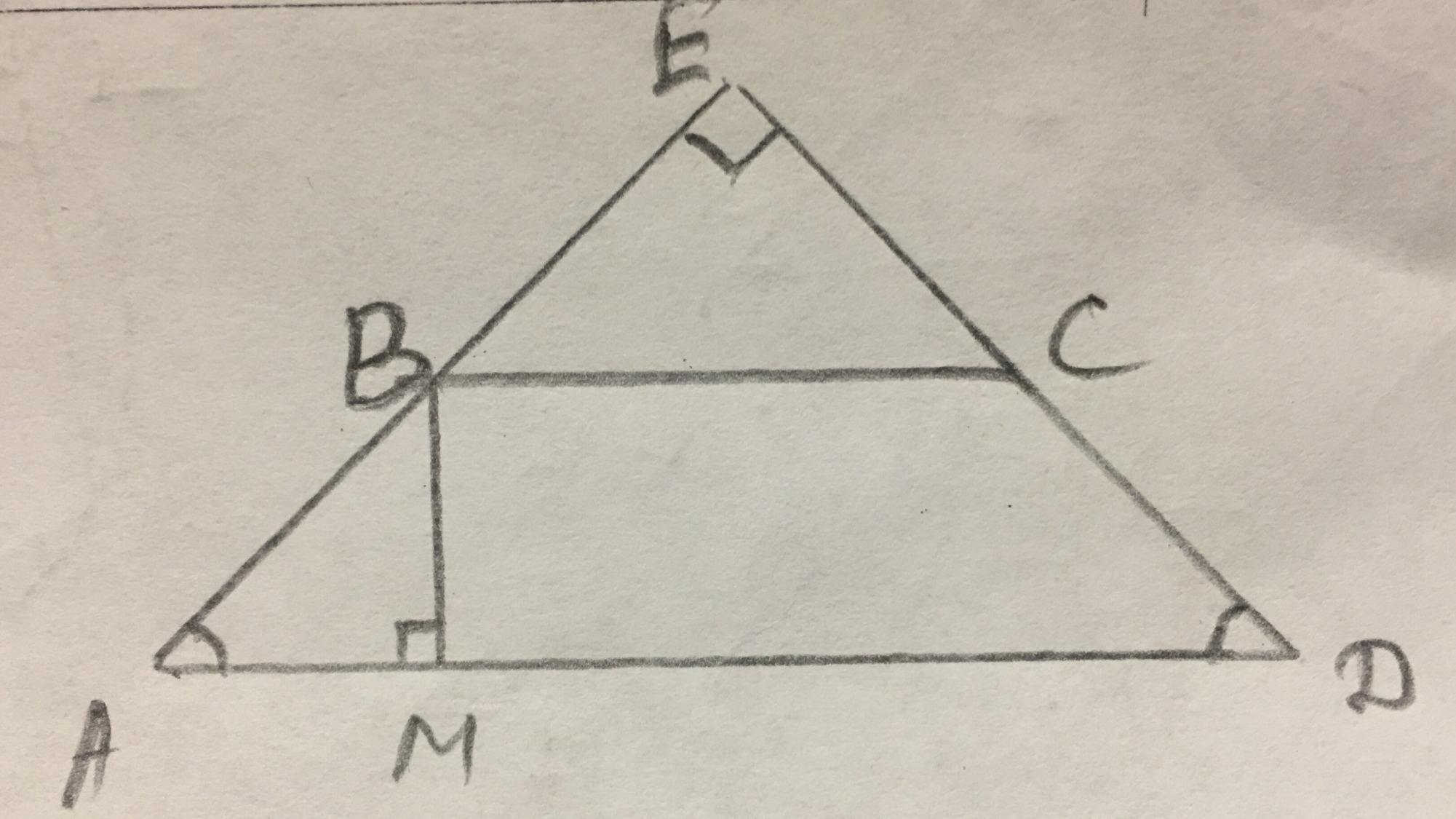
В трапеции АВСД АД=а, ВС=b, ВМ=2 см, S(АВСД)=12 см².
В прямоугольном тр-ке АЕД углы при основании равны, значит он равнобедренный с острыми углами 45°.
S(АЕД)=АД²/4=а²/4,
S(BCД)=ВС²/4=b²/4,
S(АВСД)=S(АЕД)-S(BCД),
12=a²/4-b²/4,
a²-b²=48.
S(АВСД)=h(a+b)/2 ⇒ a+b=2S(АВСД)/h=2·12/2=12 см.
b=12-a.
a²-(12-a)²=48,
а²-144+24а-а²=48,
24а=192,
а=8.
АД=8 см, ВС=b=12-8=4 см.
В равнобедренной трапеции АМ=(a-b)/2=(8-4)/2=2 см.
В тр-ке АВМ АВ²=АМ²+ВМ²=2²+2²=8,
АВ=СД=√8=2√2 см.
Ответ: 8 см, 2√2 см, 4 см и 2√2 см.
В прямоугольном тр-ке АЕД углы при основании равны, значит он равнобедренный с острыми углами 45°.
S(АЕД)=АД²/4=а²/4,
S(BCД)=ВС²/4=b²/4,
S(АВСД)=S(АЕД)-S(BCД),
12=a²/4-b²/4,
a²-b²=48.
S(АВСД)=h(a+b)/2 ⇒ a+b=2S(АВСД)/h=2·12/2=12 см.
b=12-a.
a²-(12-a)²=48,
а²-144+24а-а²=48,
24а=192,
а=8.
АД=8 см, ВС=b=12-8=4 см.
В равнобедренной трапеции АМ=(a-b)/2=(8-4)/2=2 см.
В тр-ке АВМ АВ²=АМ²+ВМ²=2²+2²=8,
АВ=СД=√8=2√2 см.
Ответ: 8 см, 2√2 см, 4 см и 2√2 см.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: surinovrahman
Предмет: Геометрия,
автор: matoxe5044
Предмет: Математика,
автор: dorrle
Предмет: Математика,
автор: катяпросио
Предмет: История,
автор: ostolopova2013