Question

Помогите по данным рисунка доказать что AD=1/3BD. Умоляю!

Answer 1

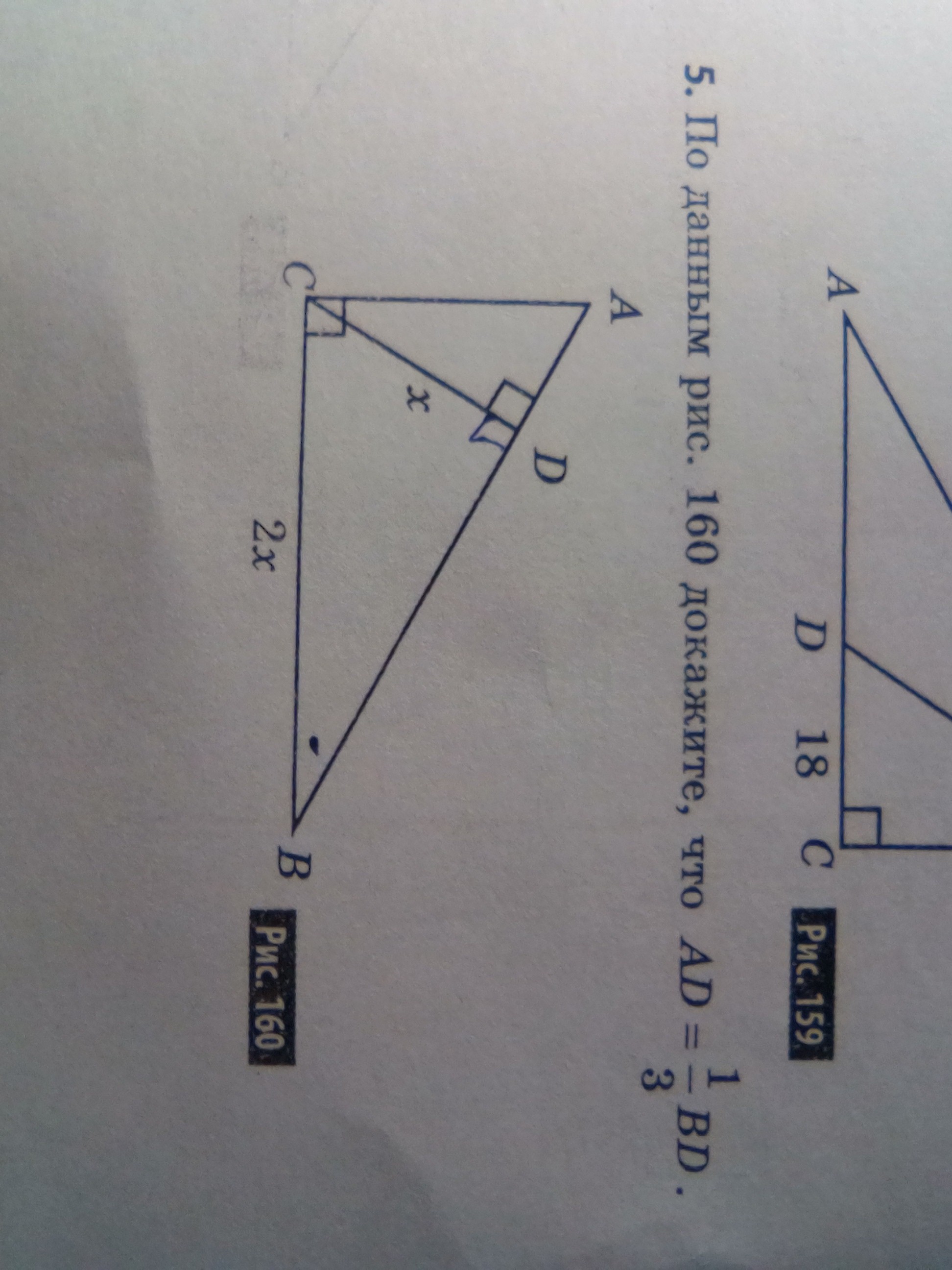
Р/м треугольник СДВ. ∠Д=90, СВ=2х, СД=х (по условию) отсюда следует по с-ву угла в 30*, что ∠В=30*, так как противолежащая сторона (СД)=2 гипотенузам (СВ).
Р/м треугольник АВС, где ∠С=90*, ∠В=30*, отсюда следует по свойству углов в треугольнике, что ∠А=60* (180-90-30).
Р/м треугольник АДС. ∠Д=90*, ∠А=60*, следовательно, ∠С=30*, отсюда уже следует, что треугольники АДС и АВС подобны по трем углам.
Вновь р/м треугольник АДС. По с-ву угла в 30* следует, что АД=1/2АС
По т. Пифагора получаем уравнение, в котором у = АД, 2у=АС
$x^{2} = y^{2} - (2y)^{2} =3 y^{2}$
$x= sqrt{3 y^{2}} = y sqrt{3}$
Теперь р/м т. Пифагора для треугольника ВСД, где z = ДВ, а $х= y sqrt{3}$
$4x^{2} - x^{2} = z^{2}$
$3 x^{2} = z^{2}$
$z= sqrt{3 x^{2} } = sqrt{3* (y sqrt{3})^{2} } = sqrt{3* y^{2}*3 } = sqrt{9 y^{2} } =3y$
т.к у - это обозначение для АД, а z для ДВ, то следовательно, 3АД=ДВ или АД=1/3ДВ