Предмет: Геометрия,
автор: Nickname13
Найдите сторону квадрата, вписанного в окружность радиусом 32 в корне
Ответы
Автор ответа:
0
Ответ:
8
Объяснение:
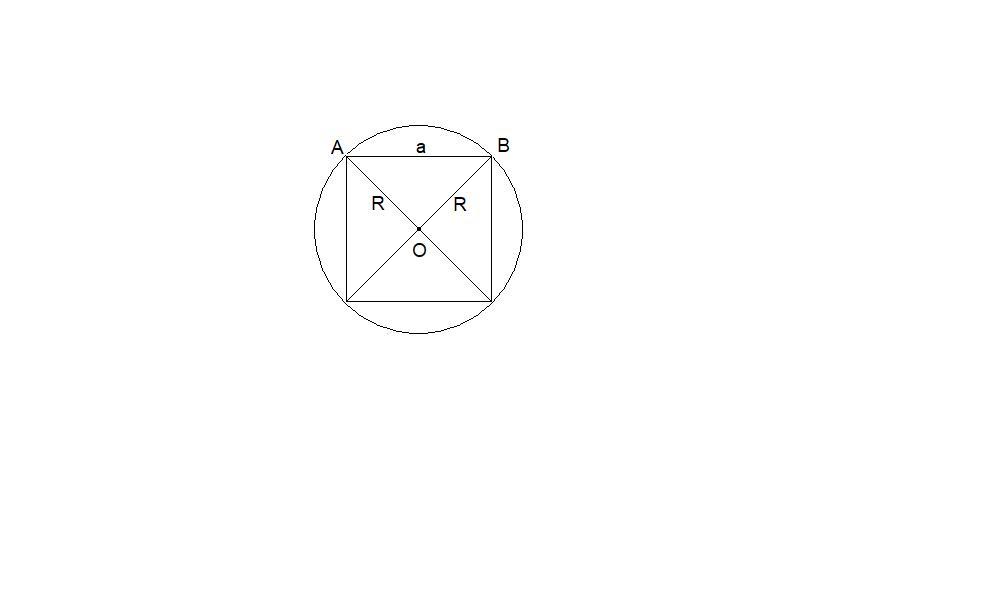
Диагонали квадрата перпендикулярны, равны и точкой пересечения делятся пополам.
Центр описанной окружности находится в точке пересечения диагоналей.
Тогда треугольник АОВ прямоугольный, равнобедренный.
a² = R² + R²
a² = 2R²
a = R√2 = √32 · √2 = √64 = 8
Приложения:
Похожие вопросы
Предмет: Математика,
автор: daniilfokin1995
Предмет: Геометрия,
автор: uk8jcnajps
Предмет: Математика,
автор: daniilfokin1995
Предмет: Биология,
автор: 20Elizaveta02