Предмет: Математика,
автор: daniilfokin1995
Точки K и N делят стороны треугольника АВС в отношении AF:FС= 5 и CN:NB= 0,6. Отрезки AN и BK пересекаются в точке M. Найдите отношение площадей треугольников AMB и MBN (ответ округлите до целого).
Ответы
Автор ответа:
1
Замечание:
В условии опечатка AF ÷ FC = 5 следует читать как AK ÷ KC
Дано:
ΔABC
AK ÷ KC = 5 ÷ 1
CN ÷ NB = 3 ÷ 5 (так как 0,6 = 3/5)
AN ∩ BK = M
Найти:
SΔAMB ÷ SΔMBN - ?
Решение:
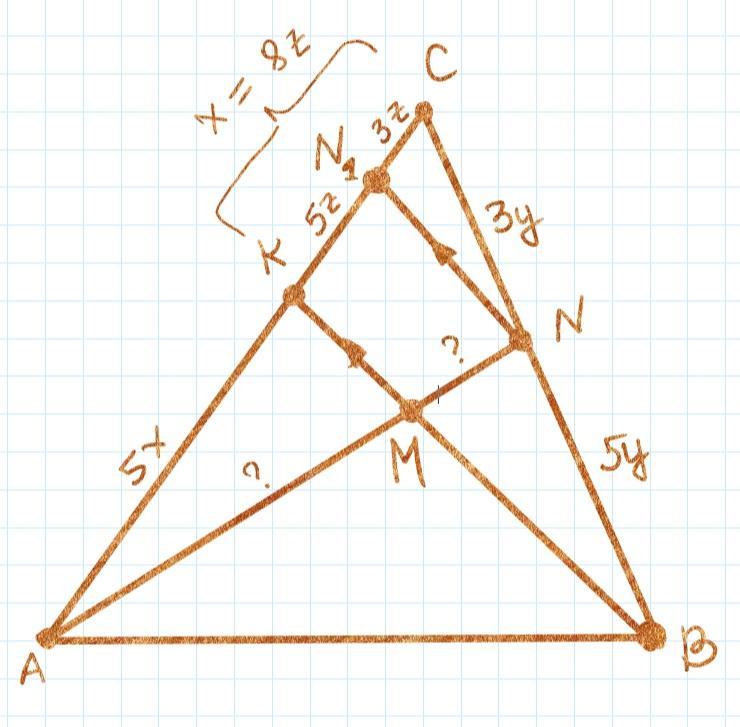
Дополнительное построение: NN₁ ║ BK (см. рисунок)
В ΔBCK:
CN₁ ÷ N₁K = CN ÷ NB (обобщенная теорема Фалеса) = 3 ÷ 5; CN = 3y; NB = 5y; CB = 8y; CN₁ = 3z; N₁K = 5z; CK = 8z; AK ÷ CK = 5 ÷ 1; AK = 5x; CK = x
поэтому 8z = x ⇒ z = 1/8 x. В итоге получаем: N₁K = 5/8 x
В ΔAN₁N: AK ÷ KN₁ = AM ÷ MN (обобщенная теорема Фалеса), поэтому
AM ÷ MN = 5x ÷ (5/8 x) = 8 ÷ 1
SΔAMB ÷ SΔMBN = AM ÷ MN (отношение площадей треугольников с общей высотой) = 8 ÷ 1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Tverk
Предмет: Русский язык,
автор: Dikomon1
Предмет: Русский язык,
автор: Andreevan366
Предмет: Русский язык,
автор: irada19