Question

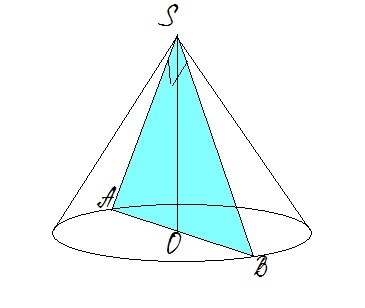
Кут при вершині осьвого перерізу конуса дорівнє 90 градусів, площа перерізу 18 см^2. Знайти об'єм конуса

Answer 1

Осьовий переріз - рівнобедрений прямокутний трикутник, $AS=SB$, $angle SAB=angle SBA = 45а$

$S= dfrac{AS^2cdot tgangle SAB}{2}$

Виразимо сторону AS, тобто маємо:

$AS= sqrt{ dfrac{2cdot S}{tg45а} } = sqrt{2cdot 18} =6$ см

$AB= sqrt{AS^2+SB^2} =6 sqrt{2}$ см - за т. Піфагора

Оскільки AB - діаметр основи, то AO - радіус основи і дорівнює половині діаметру.

$AO= dfrac{AB}{2} =3 sqrt{2}$ см

Трикутник $ASO$ - рівнобедрений прямокутний трикутник, тобто катети $AO=SO=3 sqrt{2}$ см


Знаходимо об'єм конуса.

$V= dfrac{ pi cdot AO^2cdot SO}{3} = dfrac{18 pi cdot 3 sqrt{2})}{3} =18 pi sqrt{2}$ см³


Відповідь: $18 pi sqrt{2}$ см³.