Question

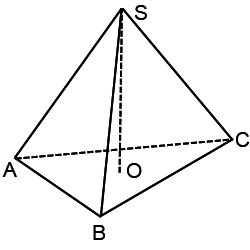
Дана правильная треугольная пирамида, высота пирамиды 6 см. Сторона основания 4 см. Найти площадь боковой грани, площадь основания, площадь полной поверхности пирамиды

Answer 1

Решение:

а = 4 cм - сторона основания

Н = 6 см - высота пирамиды

Высота треугольного основания  h = а · cos 30° = 4 · 0.5√3 = 2√3 (cм)

Точка О находится на расстоянии h/3 от стороны основания

h/3 = 2√3 : 3 = 2/√3 (cм)

Апофему боковой грани А  найдём из теоремы Пифагора

А² = H² + (h/3)²

A² = 36 + 4/3 = 112/3

A = 4 · (√(7/3) =  (4√21) /3 (см)

Площадь боковой грани

S1 = 0.5 · a · A = 0.5 · 4 ·  (4√21) /3 = (8√21) /3 (cм²) ≈ 39,6 см²

Площадь основания

Sосн = 0,5 а · h = 0.5 · 4 · 2√3 = 4√3 (см²) ≈ 6,9 см²

Площадь боковой поверхности пирамиды

Sбок = 3 S1 = 3 ·  (8√21) /3 = 8√21 (см²) ≈ 118,9 см²

Площадь полной поверхности пирамиды

S полн =  Sбок + Sосн = 8√21 + 4√ 3 ≈ 125,8 см²