Предмет: Математика,
автор: folemman
Помогите, пожалуйста, найти интеграл
Приложения:
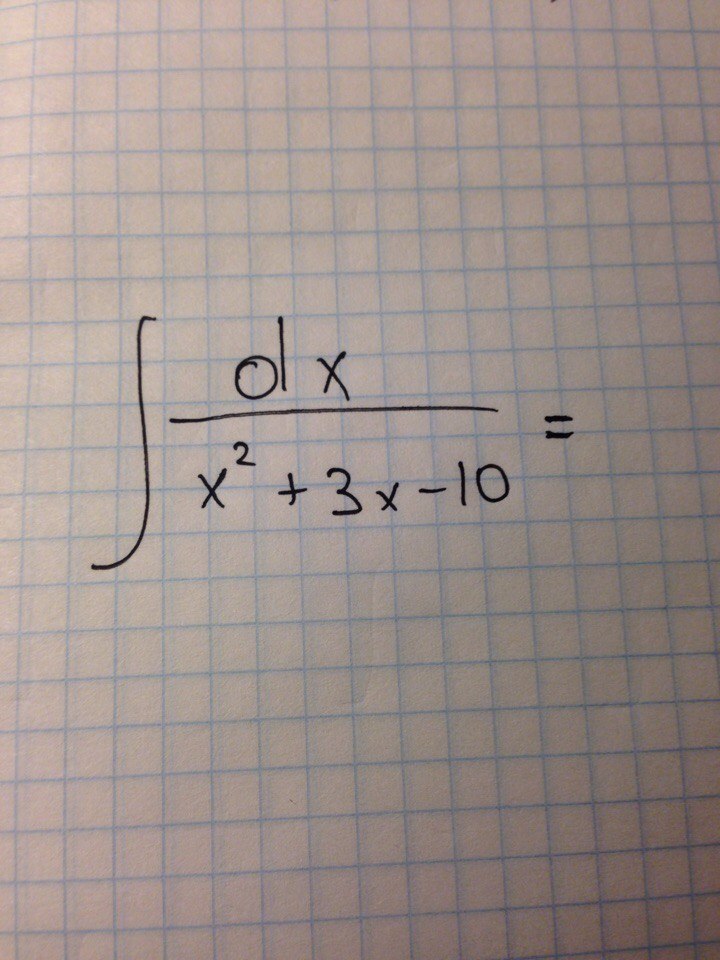
Ответы
Автор ответа:
0
Этот интеграл можно вычислять по-разному. Скажем, можно выделить полный квадрат. А можно подынтегральную функцию разложить на две более простые. Применю второй способ. Он поможет проиллюстрировать возможность разложения на элементарные дроби без неопределенных коэффициентов.
Докажем, что

Доказывается она, конечно, элементарно. Моя задача научить писать ее, не подглядывая в шпаргалку. Имеем:

Переходим к вычислению интеграла:
 .
.
В подынтегральной функции роль a исполняет (x-2), а роль (a+k) исполняет (x+5); тем самым k=7;

поэтому получаем сумму двух интегралов


Докажем, что
Доказывается она, конечно, элементарно. Моя задача научить писать ее, не подглядывая в шпаргалку. Имеем:
Переходим к вычислению интеграла:
В подынтегральной функции роль a исполняет (x-2), а роль (a+k) исполняет (x+5); тем самым k=7;
поэтому получаем сумму двух интегралов
Похожие вопросы
Предмет: Информатика,
автор: tatianamarkova905
Предмет: Физика,
автор: D2096828
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: ринас1
Предмет: Алгебра,
автор: OxxxLOLxxxO