Question

Из точки К, взятой внутри угла, равного 64 градуса, проведены две прямые, перпендикулярные сторонам угла. Найдите наименьший из возможных углов, образованных этими прямыми.+рисунок

Answer 1

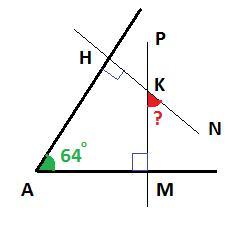
Дано : ∠A = 64°;  KH⊥AH;    KM⊥AM

Найти : ∠NKM

Решение :

Прямые KH  и  KM, перпендикулярные сторонам угла А, образуют четырёхугольник  AHKM, у которого два угла прямые. Сумма внутренних углов четырёхугольника равна 360°.

∠A + ∠AHK + ∠AMK + ∠HKM = 360°

∠HKM = 360° - ∠A - ∠AHK - ∠AMK =

          = 360° - 64° - 90° - 90° = 116°

Пересекающиеся прямые KH  и  KM образуют две пары равных вертикальных углов, меньшие из которых ∠HKP = ∠NKM.

∠HKM и ∠NKM  -  смежные углы, дают в сумме 180°

∠NKM = 180° - ∠HKM = 180° - 116° = ∠HKP = 64°

Ответ : 64°