Предмет: Алгебра,
автор: Rorymax
Помогите с интегралом!
Приложения:
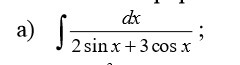
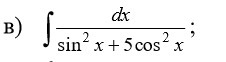
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: enicvolodina
Предмет: Математика,
автор: enicvolodina
Предмет: Математика,
автор: Kamal538
Предмет: Химия,
автор: meow9750
Предмет: История,
автор: ЕгорПрожерин