Предмет: Алгебра,
автор: Alexdhdhdhdjcd
Найдите радиус окружности, если точка А(-1;-2)-центр окружности, а В(2;2)- точка окружности
Ответы
Автор ответа:
0
Ответ ответ ответ ответ ответ
Приложения:
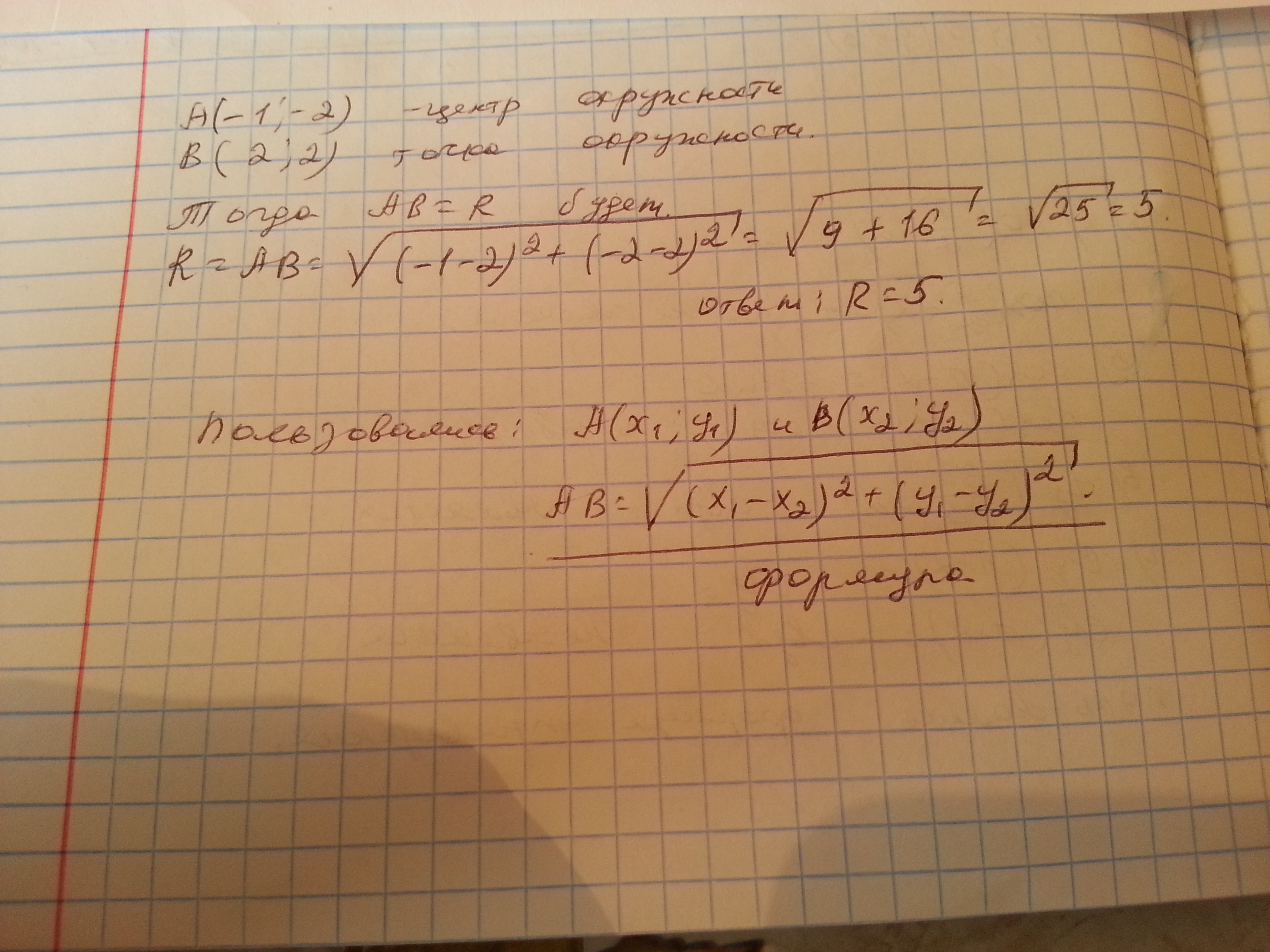
Автор ответа:
0
По формуле (х-а)^2+(y-b)^2=R^2 мы можем найти радиус R.
Для этого подставляем данные в формулу, зная, что A(-1;-2) - точка с координатами центра окружности, а B(2;2), соответственно, та точка, через которую и проходит окружность.
Тогда:
(-1-2)^2+(-2-2)^2=(-3)^2+(-4)^2=9+16=25 ( нашли R^2)
Т.к. R^2=25, то, следовательно, радиус R равен √R^2 , что является 5 (√25=5)
Ответ: R=5
Для этого подставляем данные в формулу, зная, что A(-1;-2) - точка с координатами центра окружности, а B(2;2), соответственно, та точка, через которую и проходит окружность.
Тогда:
(-1-2)^2+(-2-2)^2=(-3)^2+(-4)^2=9+16=25 ( нашли R^2)
Т.к. R^2=25, то, следовательно, радиус R равен √R^2 , что является 5 (√25=5)
Ответ: R=5
Приложения:
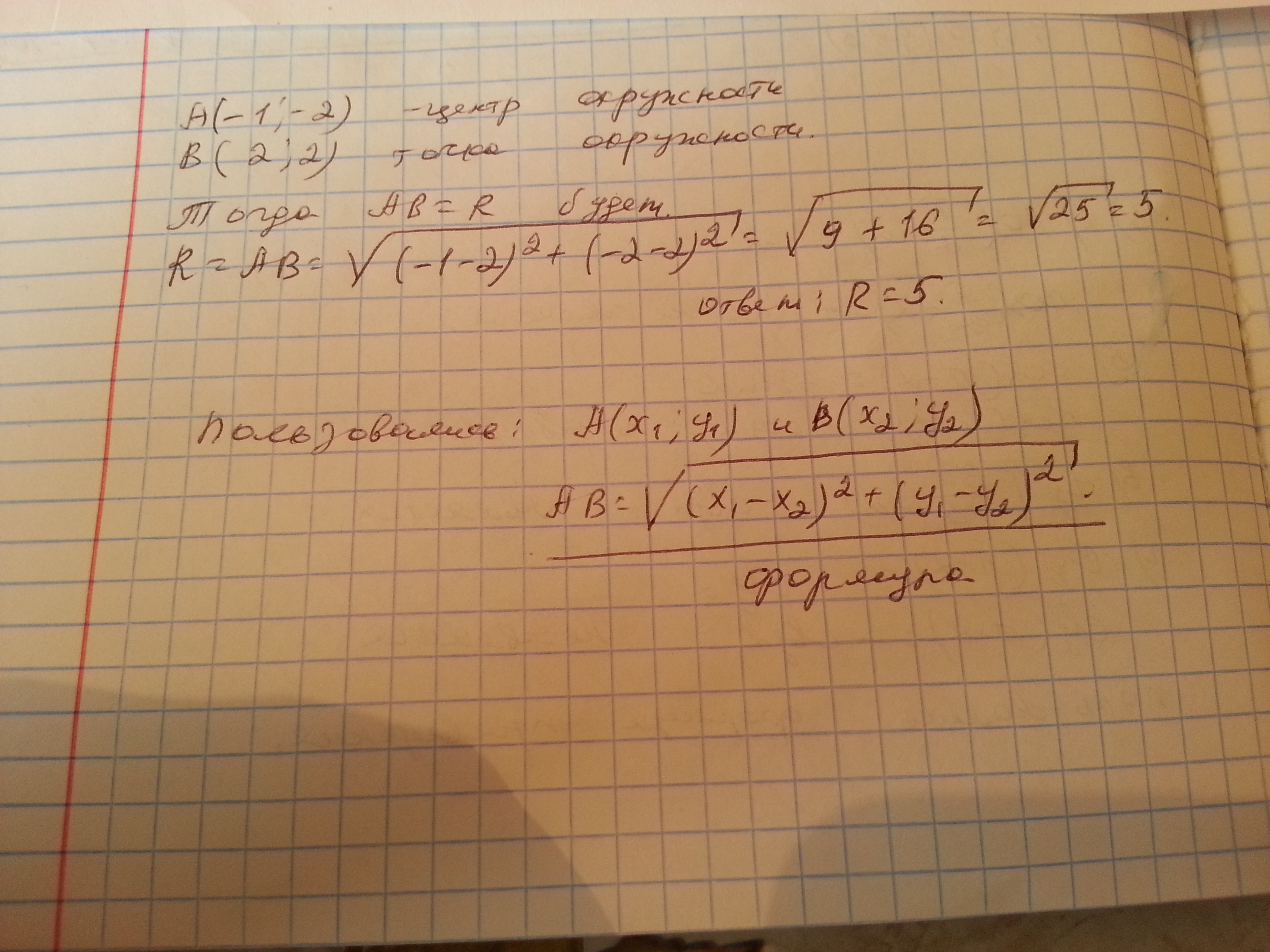
Похожие вопросы
Предмет: Алгебра,
автор: arturkobakov303
Предмет: Алгебра,
автор: arturkobakov303
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: Gulnara1993
Предмет: Математика,
автор: natka011