Question

Помогите решить уравнение: 5^|x-1|=0,2^|x+3|

Answer 1

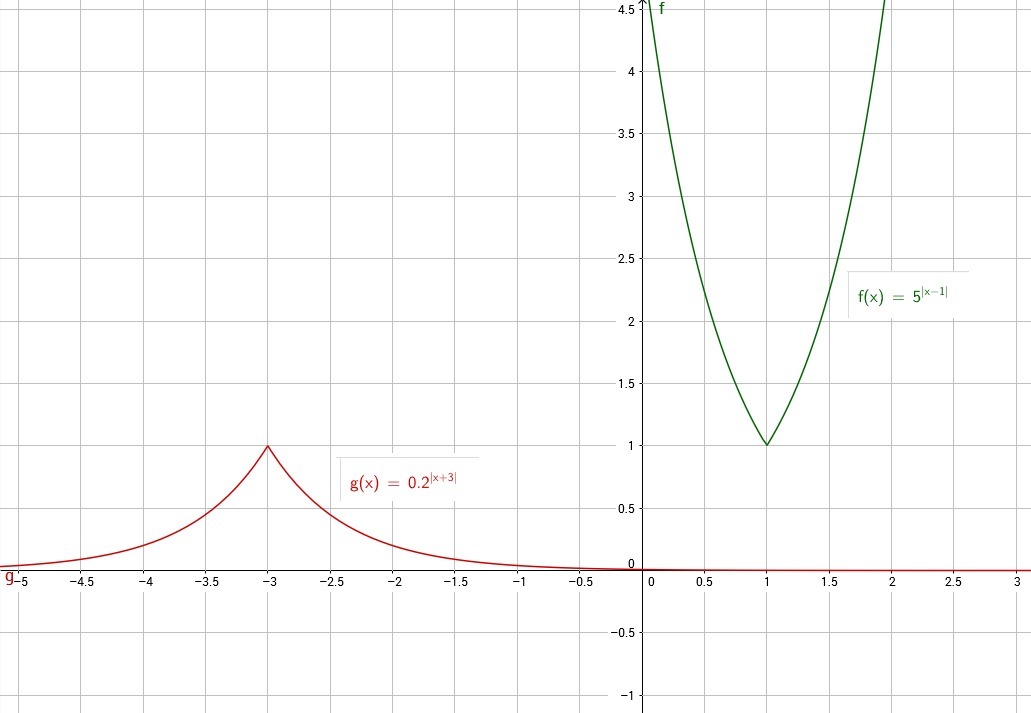
Решим графически и убедимся в том, что данные графики не пересекаются, а значит и не имеют общих решений  

Answer 2

 5^|x-1|=0,2^|x+3|
 5^|x-1|=(1/5)^|x+3|
5^|x-1|=5^(-|x+3|)
|x-1|=-|x+3|
|x-1|+|x+3|=0
так как модуль всегда больше равен 0 то оба модуля =0
x=1  x=-3 такого не может быть
Решений нет