Question

Решите задачи:
1) Катет прямоугольника равен 6 см а гипотенуза 9 см. Найдите проекцию данного катета на гипотенузу,
2) В прямоугольном треугольнике гипотенуза равна 37 см а один из катетов 35 см. Найдите периметр треугольника.
3) Диагонали ромба равна 4 см и 20 см. Найдите сторону ромба.

ПЛИЗЗЗЗЗЗЗЗ ПОБЫСТРЕЕЕЕЕЕ СРОЧНОО НУЖНОООООООО

Answer 1

Ответ:

1. 4 см.

2. 84 см.

3. 2√26 см.

Объяснение:

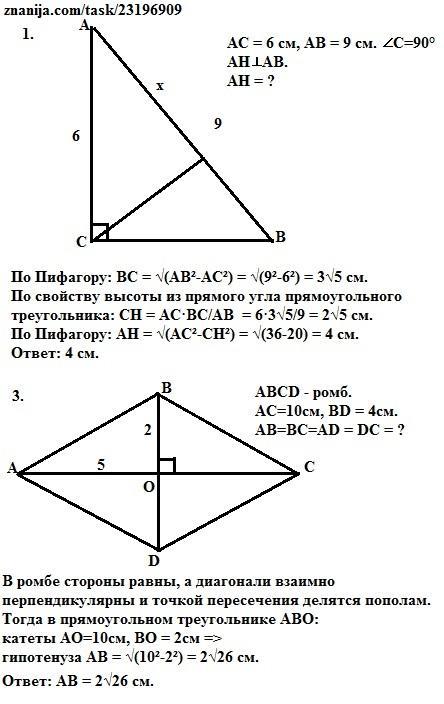
1. По Пифагору: ВС = √(АВ²-АС²) = √(9²-6²) = 3√5 см.

По свойству высоты из прямого угла прямоугольного треугольника:

СН = АС·ВС/АВ  = 6·3√5/9 = 2√5 см.

По Пифагору: АН = √(АС²-СН²) = √(36-20) = 4 см.

Ответ: 4 см.

2. По Пифагору второй катет равен √(37²-35²) = √(2·72) = 12см. Тогда периметр треугольника (сумма его трех сторон) равен:

37+35+12 = 84см.

Ответ: 84см.

3. В ромбе стороны равны, а диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.

Тогда в прямоугольном треугольнике АВО:

катеты АО=10см, ВО = 2см =>

гипотенуза АВ = √(10²-2²) = 2√26 см.

Ответ: 2√26 см.