Предмет: Геометрия,
автор: BPS
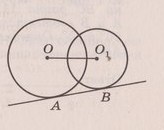
К двум пересекающимся окружностям радиусов 12 и 4 см проведена касательная. Найдите расстояние между центрами окружностей, если отрезок АВ касательной равен 17 см.
Приложения:
Ответы
Автор ответа:
0
Т.к. АВ - касательная в обеим окружностям, то она перпендикулярна ОА и О1В, значит ОА параллельно О1В и значит АВО1О - прямоугольная трапеция. Из точки О1 опустим перпендикуляр О1С на сторону ОА и получим прямоугольный треугольник СОО1 и прямоугольник АВО1С. О1С = АВ = 17; АС = ВО1 = 4.
Рассмотрим треугольник СОО1: СО=ОА-СА=ОА-ВО1=12-4=8. По теореме Пифагора ОО1^2=CО^2+O1C^2=8^2+17^2=64+289=353/
Ответ: ОО1 = корень из 353
Похожие вопросы
Предмет: География,
автор: mashakasimova07
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: Danieldiu74750
Предмет: Биология,
автор: Полинка123456
Предмет: Математика,
автор: danil90001