Question

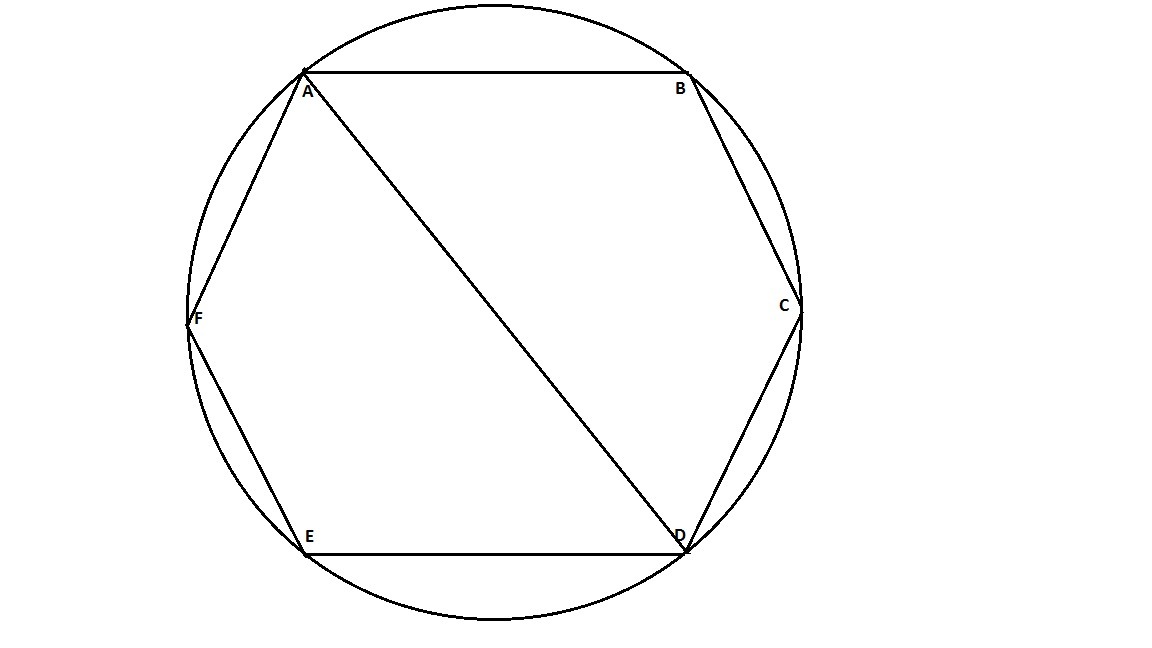
Длина окружности, описанной около правильного шестиугольника АВСDEF, равна 12пи (пи-число). Найдите площадь четырехугольника ABCD.

Answer 1

Радиус описанной окружности около правильного шестиугольника, равен стороне правильного шестиугольника.
Длина окружности равна:
$C = 2 pi R$, откуда 
$R = frac{C}{2 pi } = frac{12 pi }{2} = 6$.
Площадь правильного многоугольника измеряется по формуле:
$S = frac{1}{2}Pr$
$P = 6a = 6R = 36.$
Радиус вписанной окружности равен:
$r = Rfrac{ sqrt{3} }{2} = frac{6 sqrt{3} }{2} = 3 sqrt{3} .$
Площадь шестиугольника равна
$S = frac{1}{2}Pr = frac{1}{2}*36*3 sqrt{3} = 54 sqrt{3}$
Диагональ AD разделила шестиугольник на две равновеликие фигуры, поэтому $S_{ABCD} = frac{1}{2}S_6 = frac{1}{2}*54 sqrt{3} = 27 sqrt{3}$