Question

Найдите наименьшее целое решение неравенства:
(x+8)(x^2-22x+40)/(x^4-64x^2 )≥0.

Answer 1

$frac{(x + 8)(x^2 - 22x + 40)}{x^4 - 64x^2} geq 0$

Решим квадратное уравнение в числителе:
$x^2 - 22x + 40 = 0 \ x_1 + x_2 = 22 \ x_1*x_2 = 40 \ \ x_1 = 20\ x_2 = 2$

$frac{(x + 8)(x-2)(x - 20)}{x^4 - 64x^2} geq 0 \ \ frac{(x + 8)(x-2)(x - 20)}{x^2(x^2 - 64)} geq 0 \ \ frac{(x + 8)(x-2)(x - 20)}{x^2(x - 8)(x + 8)} geq 0 \ \ frac{(x-2)(x - 20)}{x^2(x - 8)} geq 0$
(Точка x = -8 выбивается из решения)
Нули  числителя: x = 2, 20.
Нули знаменателя: x = 0, 8
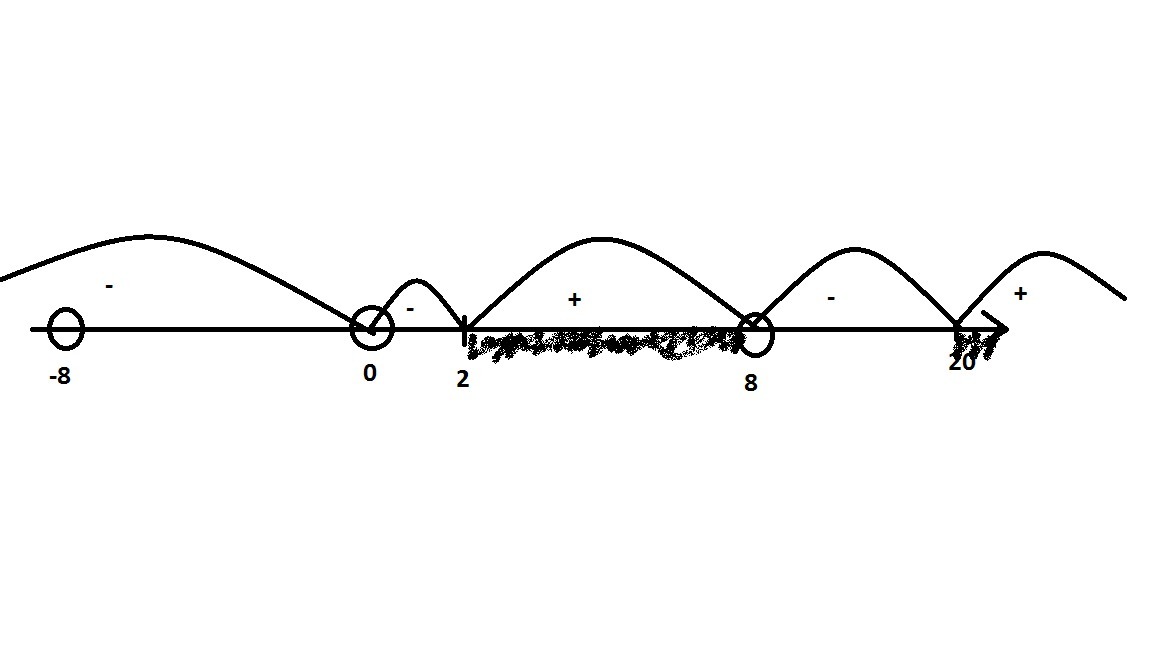
Решением неравенство служит область x ∈ [2; 8) ∪ [20; +∞)
Наименьшее целое решение  - это 2.
Ответ: 2.