Предмет: Алгебра,
автор: Satkalieva
Решите Логарифмическое неравенство. Подробно.
Приложения:
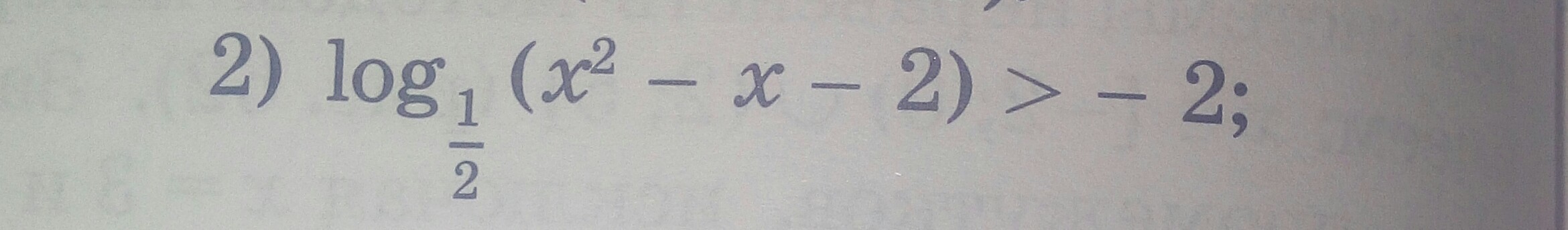
Ответы
Автор ответа:
0
Так как функция убывает (в основании логарифма лежит число меньшее 1),то знак неравенства меняется на противоположный
-2 мы представляем как ㏒ 1/2 4
㏒ 1/2(x²-x-2)< ㏒ 1/2 4
Логарифмы как бы сокращаются
x²-x-2<4
x²-x-6<0
x²-x-6=0
D=1+24
√25=5
x1=1+5/2=6/2=3
x2=1-5/2=-4/2=-2
x<-2 x<3
Ответ:(-∞;-2)
-2 мы представляем как ㏒ 1/2 4
㏒ 1/2(x²-x-2)< ㏒ 1/2 4
Логарифмы как бы сокращаются
x²-x-2<4
x²-x-6<0
x²-x-6=0
D=1+24
√25=5
x1=1+5/2=6/2=3
x2=1-5/2=-4/2=-2
x<-2 x<3
Ответ:(-∞;-2)
Автор ответа:
0
Решите Логарифмическое неравенство Log₁/₂ (x² - x - 2) > -2 ;
=======
т.к. основание логарифма 1/2 ∈ (0 ;1) || 0<1/2<1||
то Log₁/₂ (x² - x - 2) >og₁/₂ 4 ⇔
0 < x² - x - 2 < 4 ⇔ { x² - x - 2 > 0 ; x² - x - 2 < 4 .
{ (x+1)(x - 2 )>0 ; x² - x - 6 < 0.⇔ { (x+1)(x - 2 )>0 ; (x +2)(x-3) < 0.
методом интервалов :
///////////////////// (-1) --------------(2 ) //////////////////////////////
------- (-2) ////////////////////////////////////////////// (3) ---------------
ответ : x∈ (-2; -1) ∪ ( 2 ; 3).
=======
т.к. основание логарифма 1/2 ∈ (0 ;1) || 0<1/2<1||
то Log₁/₂ (x² - x - 2) >og₁/₂ 4 ⇔
0 < x² - x - 2 < 4 ⇔ { x² - x - 2 > 0 ; x² - x - 2 < 4 .
{ (x+1)(x - 2 )>0 ; x² - x - 6 < 0.⇔ { (x+1)(x - 2 )>0 ; (x +2)(x-3) < 0.
методом интервалов :
///////////////////// (-1) --------------(2 ) //////////////////////////////
------- (-2) ////////////////////////////////////////////// (3) ---------------
ответ : x∈ (-2; -1) ∪ ( 2 ; 3).
Похожие вопросы
Предмет: История,
автор: anastasia01030807
Предмет: Математика,
автор: Andrey5131
Предмет: Алгебра,
автор: rina1512
Предмет: Алгебра,
автор: bahonny