Предмет: Алгебра,
автор: sanyatkachukbc
Помогите решить несобственные интегралы.
Приложения:
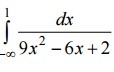
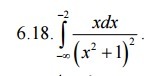
Ответы
Автор ответа:
0
Автор ответа:
0
А второе точно правильно? Просто калькулятор онлайн показывает что ответ (-1/10)
Автор ответа:
0
Да, извини, описка. Я два раза написала 1/2: один раз перед интегралом, второй в первообразной, в знаменателе, а я же уже учла её перед интегралом... Перед интегралом будет только 1/2, поэтому в ответе 1/2*1/5=1/10.
Автор ответа:
0
Спасибо.
Похожие вопросы
Предмет: Русский язык,
автор: amirgala457
Предмет: Немецкий язык,
автор: arslanjamal
Предмет: Русский язык,
автор: sabrinaelubaeva707
Предмет: Геометрия,
автор: mrdozhdik89