Предмет: Геометрия,
автор: Masha56658668
Даю 30 балов!
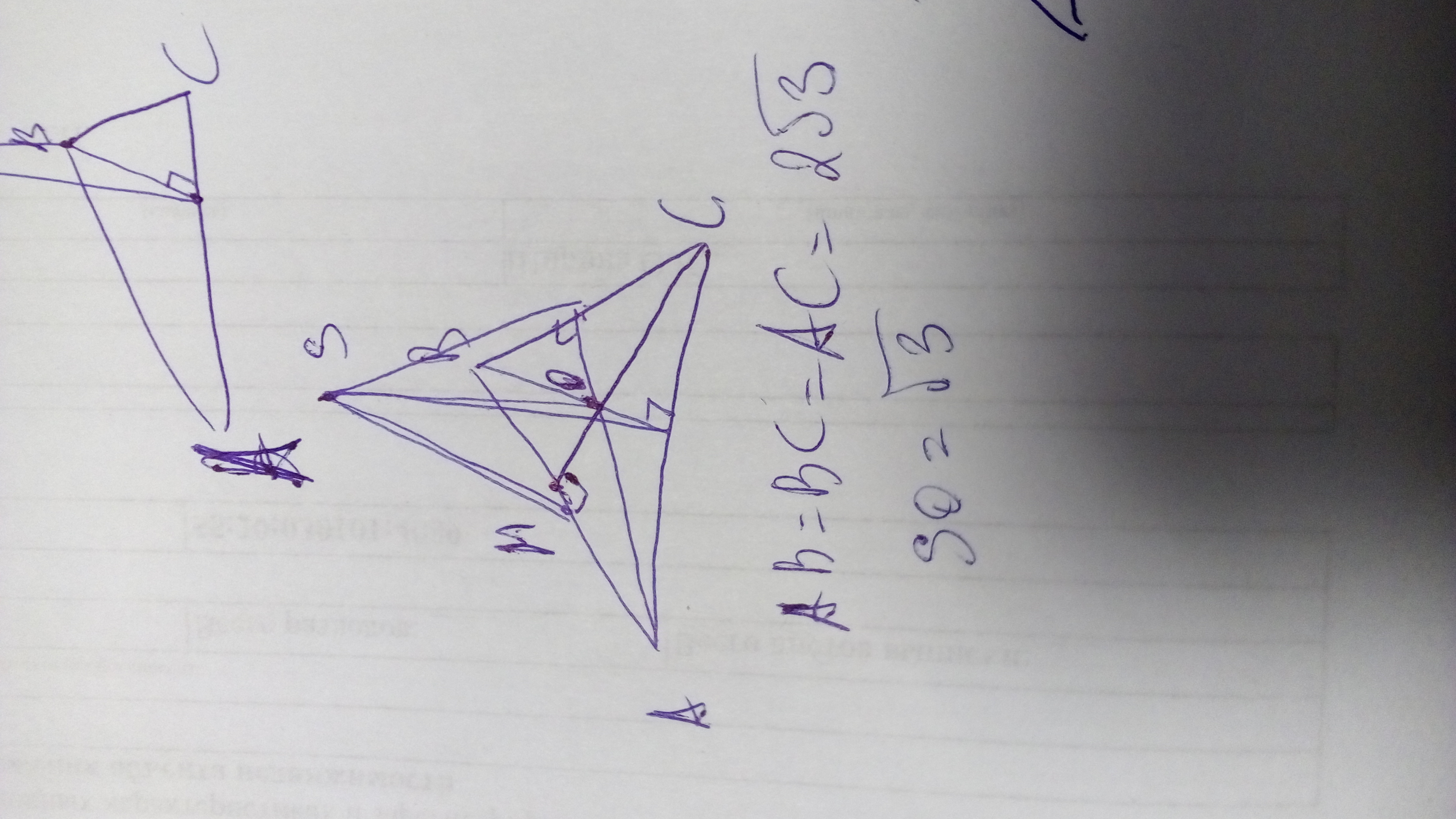
Точка S равноудаленная от каждой стороны правильного треугольника АВС, сторона которого равна 2√3см. Найдите расстояние от точки S к стороне АВ, если расстояние от точки S до плоскости АВС равна √3см.
√ - корень квадратный
Ответы
Автор ответа:
0
Вот решение.Как понял.
Приложения:


Автор ответа:
0
не видно
Автор ответа:
0
Треугольник равносторонний
точка, ближайшая ко всем сторонам в треугольнике - это точка пересечения высот треугольника. Они же являются и медианами треугольника.
Из этой точки и построен перпендикуляр, расстояние от точки S будет одновременно ближайшей к сторонам треугольника
Из треугольника АМС (прямоугольного) найдем МС по теореме Пифагора, где АМ=половине АВ
МС=√((2√3)²-(√3)²)=√(12-3)=√9=3см
По свойству пересечения высот в равностороннем треугольнике, они делятся в соотношении 1:2, т.е. МО:ОС как 1:2
следовательно МО=1см, МС=2см
из прямоугольного треугольника МОS найдем МS по теореме Пифагора
MS=√(1²+(√3)²)=√(1+3)=√4=2
ответ: расстояние от точки S к стороне АВ равно 2см
точка, ближайшая ко всем сторонам в треугольнике - это точка пересечения высот треугольника. Они же являются и медианами треугольника.
Из этой точки и построен перпендикуляр, расстояние от точки S будет одновременно ближайшей к сторонам треугольника
Из треугольника АМС (прямоугольного) найдем МС по теореме Пифагора, где АМ=половине АВ
МС=√((2√3)²-(√3)²)=√(12-3)=√9=3см
По свойству пересечения высот в равностороннем треугольнике, они делятся в соотношении 1:2, т.е. МО:ОС как 1:2
следовательно МО=1см, МС=2см
из прямоугольного треугольника МОS найдем МS по теореме Пифагора
MS=√(1²+(√3)²)=√(1+3)=√4=2
ответ: расстояние от точки S к стороне АВ равно 2см
Приложения:
Автор ответа:
0
https://znanija.com/task/22825248
Похожие вопросы
Предмет: История,
автор: luna2217
Предмет: Математика,
автор: rodionivaniscky2009
Предмет: Физика,
автор: ivanplakhtiy
Предмет: Алгебра,
автор: Катя1345
Предмет: Математика,
автор: w12345678908