Question

Около шара с радиусом r описан конус, образующая которого наклонена к плоскости основания под углом альфа. Найдите площадь осевого сечения конуса, если r=2 м, альфа- 50 градусов. Пожалуйста с рисунком!

Answer 1

Ответ:   ≈ 21,9 м²

Пошаговое объяснение:

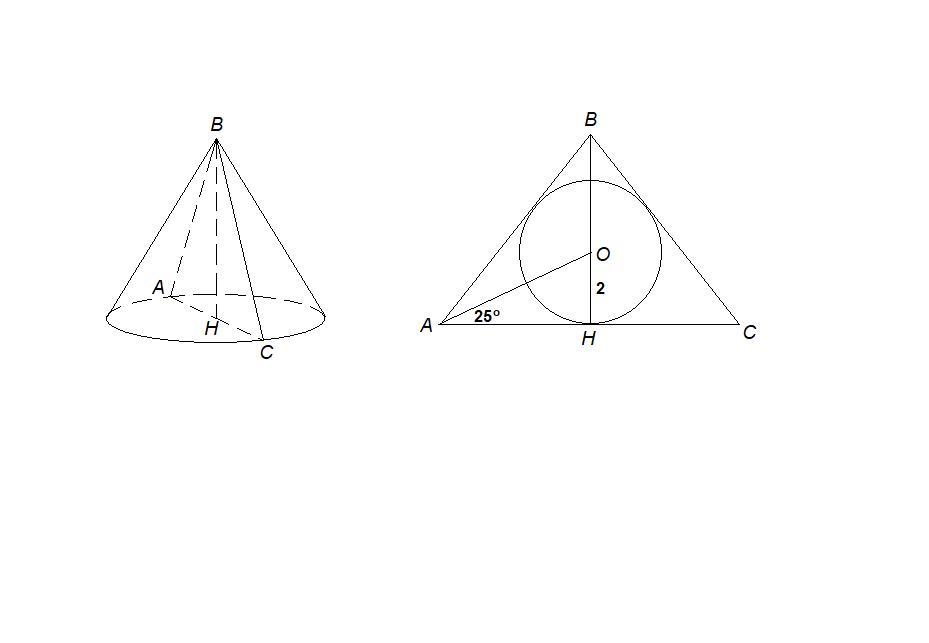
Большой круг шара вписан в осевое сечение конуса - в равнобедренный треугольник АВС.

∠А = 50°.

Центр окружности, вписанной в треугольник - точка пересечения его биссектрис. ВН - медиана равнобедренного треугольника, проведенная к основанию, значит высота и биссектриса, АО - биссектриса ∠А.

Тогда ∠ОАН = 1/2 ∠А = 25°.

ΔАОН:  ∠АНО = 90°,  ОН = r = 2 м,

             АН = ОН · ctg25° = 2·ctg25°.

AC = 2 · AH = 2 · 2·ctg25° = 4·ctg25°

ΔABH:  ∠AHB = 90°,  

            BH = AH · tg50° = 2·ctg25° · tg50°

Sabc = 1/2 · AC · BH = 1/2 · 4·ctg25° · 2·ctg25° · tg50°

Sabc = 4ctg²25° · tg50° ≈ 21,9 м²