Предмет: Алгебра,
автор: KharchenkoConst
Алгебра, 10 класс. Доказать тождество: (sin(t)) / (4cos(t/2)cos^2(t/4)) = tg(t/4)
Это то, к чему я пришёл. Начальное уравнение во вложении.
Приложения:
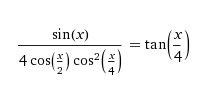
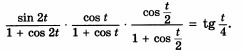
Ответы
Автор ответа:
0
sinx=2sin(x/2)cos(x/2)
2sin(x/2)cos(x/2)/4cos(x/2)*cos²(x/4)=sin(x/2)/2cos²(x/4)=sin(x/2)/1+cosx/2 понизил степень
2sin(x/4)cos(x/4)/sin²(x/4)+cos²(x/4)+cos²(x/4)-sin²(x/4)=2sin(x/4)cos(x/4)/2cos²(x/4)=sin(x/4)/cos(x/4)=tg(x/4) Вроде подробно!
2sin(x/2)cos(x/2)/4cos(x/2)*cos²(x/4)=sin(x/2)/2cos²(x/4)=sin(x/2)/1+cosx/2 понизил степень
2sin(x/4)cos(x/4)/sin²(x/4)+cos²(x/4)+cos²(x/4)-sin²(x/4)=2sin(x/4)cos(x/4)/2cos²(x/4)=sin(x/4)/cos(x/4)=tg(x/4) Вроде подробно!
Автор ответа:
0
Автор ответа:
0
Это всё берётся из формулы двойного угла
Автор ответа:
0
sin(t/2)=2sin(t/4)cos(t/4)
Автор ответа:
0
sin2a = 2sina*cosa
Автор ответа:
0
также со всеми формулами можно сделать
Похожие вопросы
Предмет: Химия,
автор: ilyafffix
Предмет: Математика,
автор: artembogdanovic8
Предмет: Математика,
автор: baurkurmet86
Предмет: Алгебра,
автор: alinashukurbek
Предмет: Алгебра,
автор: daniilkirsanov