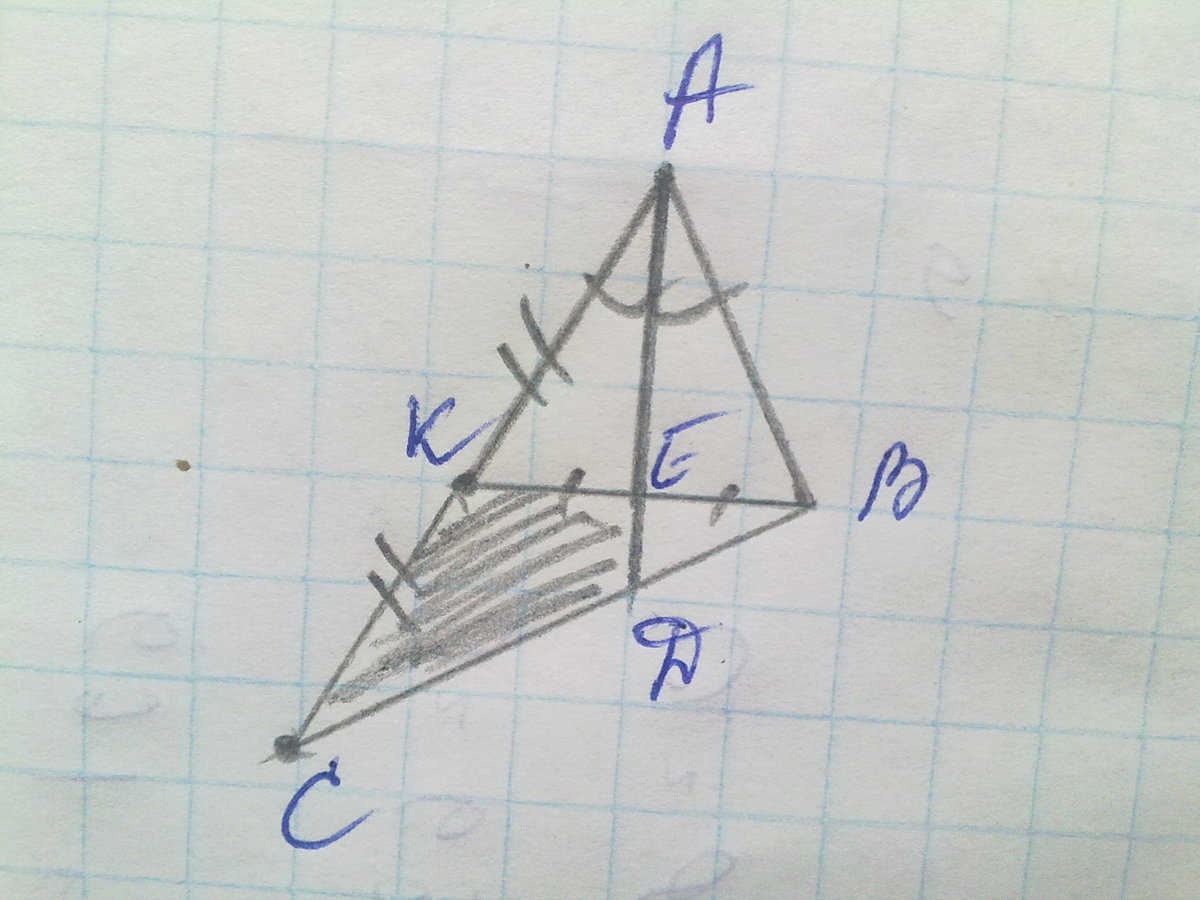
Площадь треугольника АВС = 60, AD - биссектрисса, пересекает медиану BK в точке E, причем BE = KE Найти площадь четырехугольника EDCK
S тр.BKC = S тр.BKA = 30,так как у них основания AK = KC по св-ву медианы.
при этом S тр.KAE = S тр.AEB = 15, у них тоже основания равны из условия
И скорее всего, медиана и биссектрисса пересекаются под углом в 90 градусов, как это доказать?
Может тут какое специфичное свойство биссектриссы нужно еще применять?
Ответы
В треугольнике АКВ биссектриса АЕ является еще и медианой, а это значит , что треугольник АКВ равнобедренный и АЕ является также высотой. Отсюда следует, что треугольники АВЕ и АКЕ прямоугольные и равны по двум катетам(КЕ=ЕВ по условию, АЕ-общий), значит АК=АВ и площади этих треугольников равны.
Рассмотрим теперь треугольники АВD и АСD. Они имеют по равному углу.
Площади треугольников, имеющих равные углы (или общий угол), относятся как произведения сторон, содержащих этот угол.
Значит площадь треугольника АСD относится к площади АВD как 2:1(т.к. АС=2АВ, АD- общая сторона). Значит площадь АСD=40, площадь АВD=20 =>площадь ЕВD=5.
ПОлучаем, что площадь СКЕD=60-30-5=25
Ответ: 25