ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ!ОЧЕНЬ НУЖЕН ОТВЕТ С РЕШЕНИЕМ!
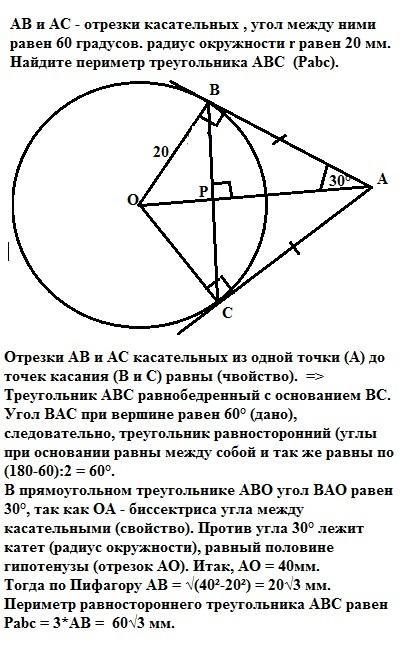
АВ и АС - отрезки касательных , угол между ними равен 60 градусов. радиус окружности r равен 20 мм. Найдите Р ФВС
Ответы
Отрезки АВ и АС касательных из одной точки (А) до точек касания (В и С) равны (свойство). =>
Треугольник АВС равнобедренный с основанием ВС.
Угол ВАС при вершине равен 60° (дано), следовательно, треугольник равносторонний (углы при основании равны между собой и так же равны по (180-60):2 = 60°.
В прямоугольном треугольнике АВО угол ВАО равен 30°, так как ОА - биссектриса угла между касательными к окружности (свойство). Против угла 30° лежит катет (радиус окружности), равный половине гипотенузы (отрезок АО). Итак, АО = 40мм.
Тогда в треугольнике АОВ по Пифагору АВ = √(40²-20²) = 20√3 мм.
Периметр равностороннего треугольника АВС равен
Pabc = 3*АВ = 60√3 мм.