Question

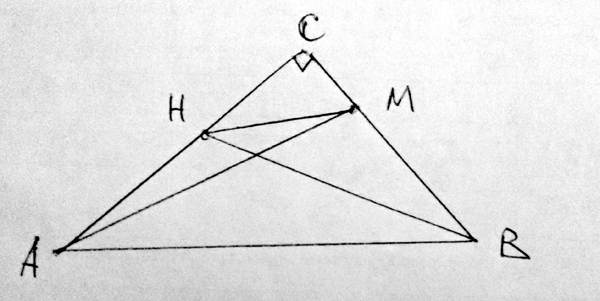
гипотенуза AB прямоугольного треугольника ABC равна x. Произвольная точка M на катете BC соединена с вершиной A, а точка H на катете AC соединена с вершиной B. найдите длину отрезка MH, если AM(в квадрате) +BH(в квадрате) =y(в квадрате)

Answer 1

Соединим вершину треугольника А с точкой М и вершину В с точкой Н.
Из прямоугольного треугольника НСМ: МH^2=CH^2+CM^2.
Из прямоугольного треугольника ACM: CM^2=AM^2-AC^2.
Из прямоугольного треугольника BCH: CH^2=BH^2-BC^2.
Поэтому МH^2 = AM^2-AC^2+BH^2-BC^2 = AM^2+BH^2-(AC^2+BC^2).
По условиям задачи AM^2+BH^2=y^2.
Из прямоугольного треугольника АВС: AC^2+BC^2=AB^2=x^2.
Поэтому МH^2=y^2-x^2;
MH=$sqrt{y^2-x^2}$.