Предмет: Алгебра,
автор: tupoyfg
как решить вот это ?
Приложения:
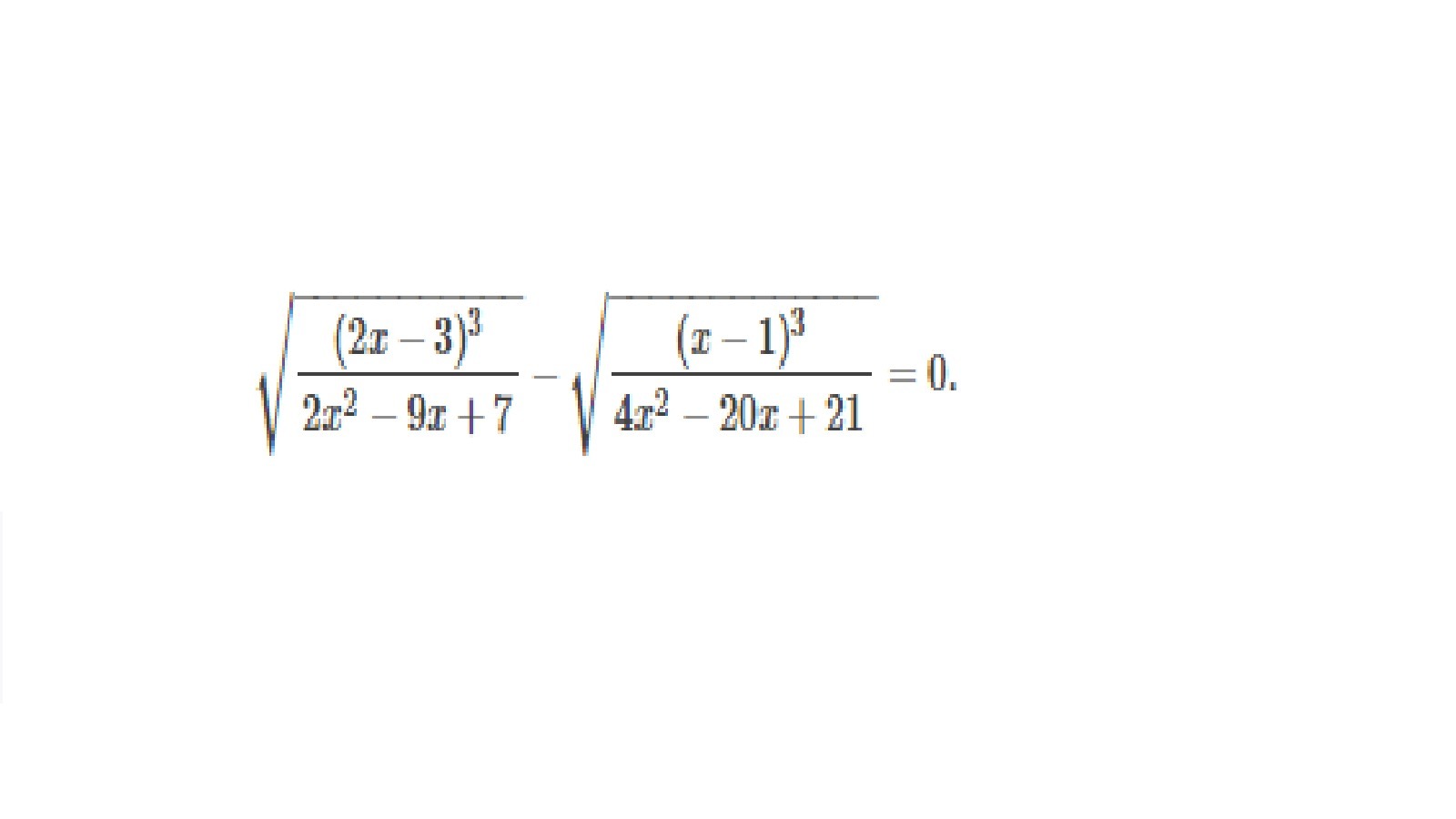
Ответы
Автор ответа:
0
*********************************
Приложения:



Автор ответа:
0
- + - +
---------[1]------------(1.5)-----------(3.5)---------------
//////////////// /////////////////////
ОДЗ:
∅ ∅ ∅
Ответ:
Приложения:



Похожие вопросы
Предмет: Русский язык,
автор: forhiifrhjj
Предмет: Биология,
автор: vxxlam
Предмет: Математика,
автор: prokhorlol57
Предмет: История,
автор: dumin88
Предмет: Математика,
автор: Аноним