Question

Средняя линия равнобокой трапеции в каторую можно вписать окружность
=12см. найти боковую сторону трапеции.

Answer 1

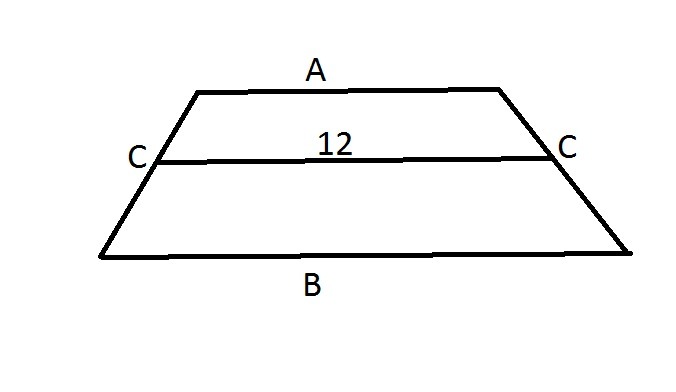
Мы знаем, что средняя линия трапеции равна полусумме оснований самой трапеции. Возьмем основания трапеции как А и В, а боковую сторону как С. Из средней линии получаем, что (А+В)/2=12. Так же мы знаем свойство описанной трапеции, которое гласит, что суммы противоположных сторон равны. А+В=С+С.
Теперь возьмем первое выражение.
(А+В)/2=12
А+В=24
Теперь заменяем А+В из первого во второе выражение.
24=2*С
С=12

Answer 2

Так в трапеции не 3 точки..должны вроде быть 4 АВСД

Answer 3

Нет. Я взял не точки, а стороны за А, В, С. Так как боковые стороны равны, они обе равняются С. Это неизвестные такие

Answer 4

Ок

Answer 5

Сейчас прикреплю рисунок. Я думал, что он не понадобится и его не прикрепил.

Answer 6

- в равнобедренную трапецию можно вписать окружность, если боковая сторона равна  средней линии. 

- 2R = h

опустим высоту. она образует прямоугольный треугольник с углами 90, 30 и 60 гр. ⇒ h=1/2*стороны = 1/2*4=2 дм

S(трап)=ср. линия*высоту = 4*2=8дм²

S(круга)= πR²=1²*π=π