Question

Помогите с касательной к графику функции. Заранее спасибо)

Answer 1

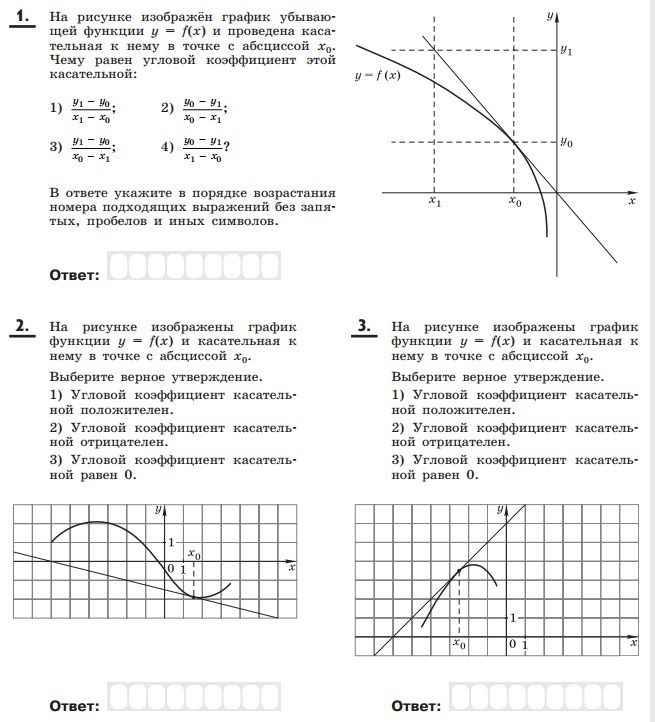
1. При переходе из точки x0 в точку x1 аргумент получает отрицательное приращение Δx<0. Функция же при этом получает положительное приращение Δy>0, Поэтому производная y'(x0)=lim Δy/Δx<0. А так как угловой коэффициент касательной в точке (x0,y0) k=y'(x0), то k<0. Этому условию удовлетворяет как выражение 1), так и тождественное ему выражение 2). Ответ: 1) и 2).

2) В данной точке функция убывает. поэтому y'(x0)<0. А так как k=y'(x0), то k<0. Ответ: k <0.

3) В точке x0 функция возрастает, поэтому k=y'(x0)>0. Ответ: k>0.